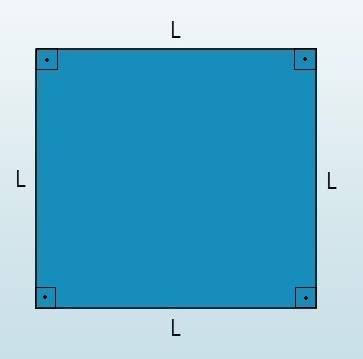
A polygon is regular when it is convex and has all sides and angles of the same measure. Therefore, a regular polygon is equilateral, since all sides are the same length, and equiangular, since all angles are the same measure.
The definition of a polygon is a closed, flat figure formed by non-aligned and non-intersecting line segments. These segments are the sides of the polygon which, when regular, are of the same length.
The meeting of two sides is a vertex, and the area between the sides is called an interior angle, measured in degrees. In regular polygons the angles are congruent.
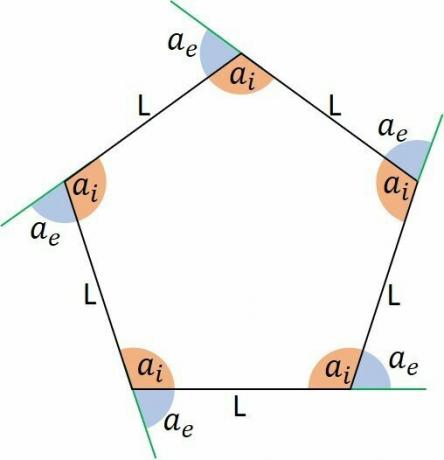
A polygon has the same number of sides, vertices, interior (ai) and exterior (ae) angles.
Regular polygons are convex, equilateral, and equiangular because their sides and angles are congruent. The three conditions must be satisfied.
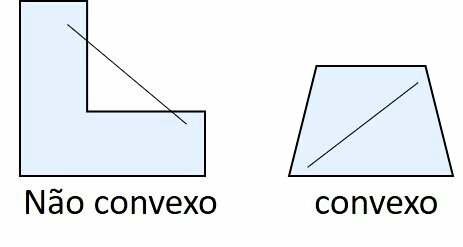
A polygon is convex when each and every segment connects two points inside it, without any part of the segment falling outside the area of the polygon.
Perimeter of regular polygons
The perimeter of a polygon is the sum of the measures of its sides. As in a regular polygon, all sides have the same length, just multiply the length of one side by the number of sides of the polygon.
Where,
P is the perimeter,
n is the number of sides,
L is the length of the sides.
Example
The perimeter of a regular hexagon with sides of 7 cm is:
interior angles
An interior angle is the region formed between two sides that meet at a vertex. In a regular polygon, all interior angles are of the same measure.
Likewise, if the value of the sum of angles is known, the measure of an angle is the total divided by the number of angles.
Sum of polygon interior angles
If the measure of an interior angle is known, you can determine the sum of the interior angles by multiplying its value by the number of angles.
Where: is the sum of the interior angles of the polygon;
is the measure of an interior angle;
n is the number of interior angles.
To determine the sum of the interior angles of a polygon without knowing the measure of an angle, we use the formula:
Example
The sum of the interior angles of a regular polygon with 6 sides and the measure of each angle is:
.
The measure of each angle is
.
Apothem of a regular polygon
The apothem of a regular polygon is a line segment that joins the center of the polygon to the midpoint of a side, making it an angle of 90°.

In this way, the apothem divides a side into two equal parts, being a bisector, because it divides the side exactly in half.
The number of apothems of a polygon is the same as its number of sides. As the polygon is regular, the apothems have the same measure.
Area of regular polygons
One way to calculate the area of any regular polygon, regardless of its number of sides, is to multiply its semiperimeter by its apothem.
The semiperimeter is half the perimeter.
Where,
P is the semiperimeter (perimeter divided by two)
The is the measure of the apothem.
Example
A regular hexagon with a side length of 4 cm and apothem cm has as area:
Resolution
The area can be calculated as the product of the apothem and the semiperimeter.
Since a hexagon has 6 sides, its perimeter is 6.4 = 24 cm and its semiperimeter is 24/2 = 12 cm.
So the area is
See more about area and perimeter.
Regular polygon exercises
Exercise 1
Classify polygons as regular and non-regular.
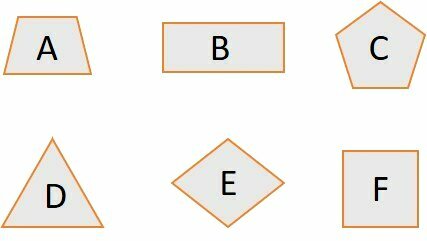
A: not regular.
B: not regular.
C: regular.
D: regular.
E: not regular.
F: regular.
Exercise 2
Find the sum of the interior angles of a regular 10-sided polygon and the measure of each angle.
The sum of the angles is determined by:
Since the polygon is regular, to determine the measure of the angles, simply divide the total by 10.
Exercise 3
Find the area of an equilateral triangle with sides equal to cm and apothem equal to 4 cm.
The perimeter of the triangle is: .
Its semiperimeter is:
Its area is the product of the apothem and the semiperimeter.
See more at:
- polygons
- Classification of Triangles
- Area and Perimeter
- angles
- Polygon Area
- Exercises on Polygons
- Sum of the interior angles of a polygon
- Hexagon
- quadrilaterals
- parallelogram
- trapeze
- Rectangle
- Classification of Triangles
- 8th grade math exercises
- 6th grade math exercises