Two distinct lines are parallel when they have the same slope, that is, they have the same slope. Furthermore, the distance between them is always the same and they have no common points.
Parallel, concurrent and perpendicular lines
Parallel lines do not intersect. In the figure below we represent the parallel lines r and s.

Unlike parallel lines, competing lines intersect at a single point.
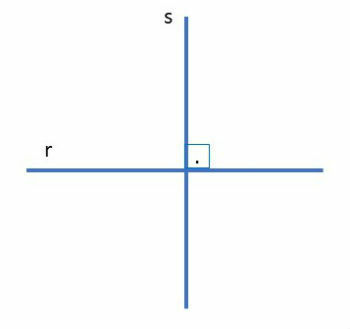
If two lines intersect at a single point and the angle formed between them at the intersection is equal to 90º, the lines are called perpendicular.
To learn more, read also:
- straight
- semi-rectal
- Line Equation
- Perpendicular Lines
- Competing Lines
- Calculation of Angular Coefficient
Parallel lines cut by a transverse
A line is transversal to another if they have only one point in common.
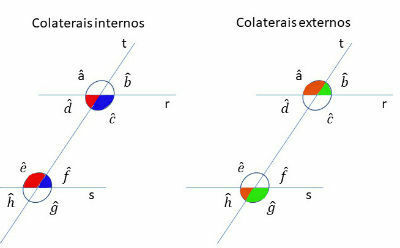
Two parallel lines r and s, if they are cut by a line t, transversal to both, will form angles as depicted in the image below.
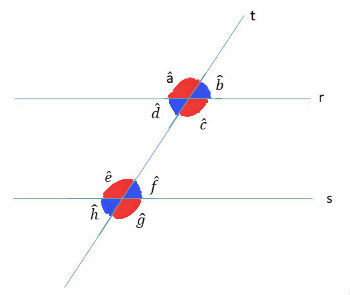
In the figure, the angles that have the same color are congruent, that is, they have the same measure. Two angles of different colors are supplementary, that is, they add up to 180º.
For example, the angles The and ç have the same measurement and the sum of the angles f and g is equal to 180º.
The pairs of angles are named according to their position in relation to the parallel lines and the transversal line. Therefore, the angles can be:
- Correspondents
- Alternates
- Collateral
corresponding angles
Two angles that occupy the same position on parallel straight lines are called corresponding. They have the same measurement (congruent angles).
The same-colored angle pairs shown below match.
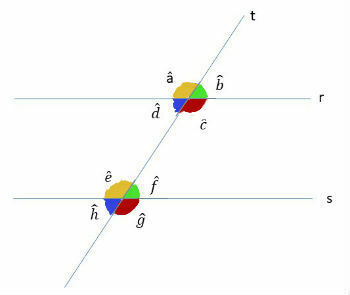
In the figure, the corresponding angles are:
- The and and
- B and f
- ç and g
- d and H
alternate angles
The pairs of angles that are on opposite sides of the transverse straight are called alternating. These angles are also congruent.
Alternating angles can be internal, when they are between parallel lines, and external, when they are outside parallel lines.

In the figure, the alternate internal angles are:
- ç and and
- d and f
The external alternating angles are:
- The and g
- B and H
side angles
These are the pairs of angles that are on the same side of the transverse straight. The collateral angles are supplementary (they add up to 180º). They can also be internal or external.
In the figure, the internal side angles are:
- d and and
- ç and f
The outside side angles are:
- The and H
- B and g
Thales' Theorem
In the same plane a bundle of parallel lines determine, in two transversal lines, straight segments proportional.
Example
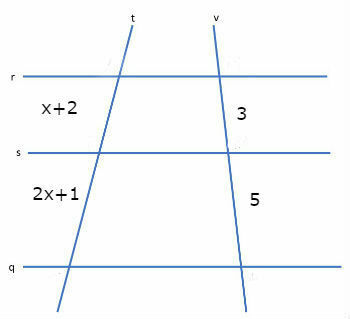
Points A, A´, B, B´, C, C´ were obtained by crossing the parallel lines r, s and q with the transversal lines t and v.
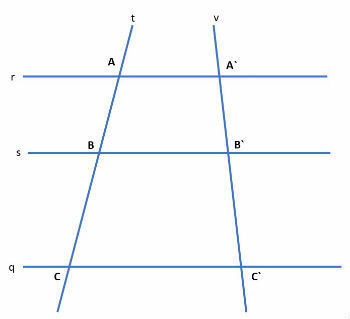
According to the Thales' theorem, we will have the following relationship:
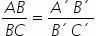
Exercises
1) Observing the angles between the parallel lines and the transverse line, determine the angles indicated in the figure:

The given angle and angle x are external collaterals, so the sum of the angles equals 180°. In this way, the measure of the angle x is 60º.
The given angle and the y angle are external alternates, therefore, they are congruent. Thus, the measure of angle y is 120°.
2) Given the figure below, find the value of the indicated angle, knowing that the lines r and s are parallel.
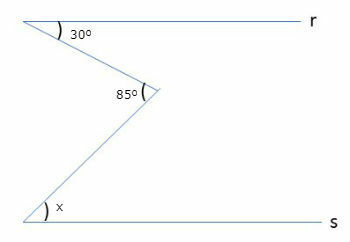
Angle x measures 55º
3) Determine the value of x in the figure below: