Sine, cosine and tangent exercises

Study with the solved sine, cosine and tangent exercises. Practice and clear your doubts with the commented exercises.

question 1

Determine the values of x and y in the following triangle. Consider sin 37º = 0.60, cosine of 37º = 0.79 and tan 37º = 0.75.

see answer

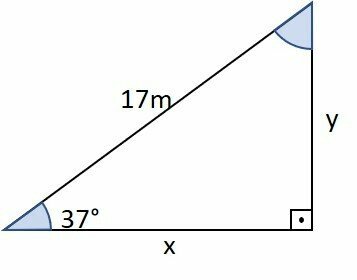
Answer: y = 10.2 m and x = 13.43 m

To determine y, we use the sine of 37º, which is the ratio of the opposite side to the hypotenuse. It is worth remembering that the hypotenuse is the segment opposite the 90º angle, so it is worth 17 m.

s and n space 37º equals y over 17 17 space. s space and n space 37º equals y 17 space. space 0 comma 60 space equals y space 10 comma 2 m space equals y space

To determine x, we can use the cosine of 37º, which is the ratio between the side adjacent to the angle of 37º and the hypotenuse.

cos space 37º equals x over 17 17 space. space cos space 37º equals x 17 space. space 0 comma 79 space equals space x 13 comma 4 m space approximately equal space x

question 2

In the following right triangle, determine the value of the angle straight tit , in degrees, and its sine, cosine, and tangent.

Consider:

sin 28º = 0.47
cos 28º = 0.88

see answer

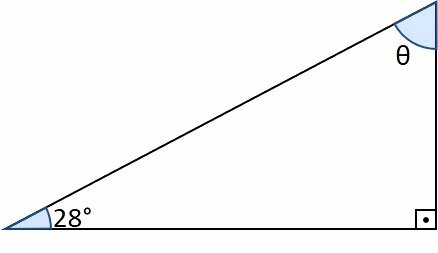
Reply: theta equals 62 degree sign , cos space 62 degree sign approximately equal 0 comma 47 comma s and n space 62 degree sign approximately equal 0 comma 88 space and space a space tan space 62 degree sign space approximately equal space 1 point 872.

In a triangle the sum of the interior angles is equal to 180°. Being a right triangle there is a 90º angle, so there are another 90º left for the two angles.

In this way we have:

28 º space plus space theta space equals space 90 º theta space equals space 90 º space minus space 28 º theta space equals space 62 º

As these angles are complementary (from one of them, the other is how much is left to complete 90º), it is valid that:

instagram story viewer

cos 62º = sin 28º = 0.47

and

sin 62º = cos 28º = 0.88

Tangent calculation

The tangent is the ratio of the sine to the cosine.

$tan space 62º space equals space numerator s and n space 62º over denominator cos space 62º end of fraction equals numerator 0 comma 88 over denominator 0 comma 47 end of fraction approximately equal 1 comma 872$

question 3

At a certain time of a sunny day, the shadow of a house is projected for 23 meters. This leftover makes 45º in relation to the ground. In this way, determine the height of the house.

see answer

Answer: The height of the house is 23 m.

To determine a height, knowing the angle of inclination, we use the tangent of the 45° angle.

The 45° tangent is equal to 1.

The house and the shadow on the ground are the legs of a right triangle.

$tan space 45 º equals numerator c a t e t o space o pos t o over denominator c a t e t o space a d j a c e n t e end of fraction equals numerator a l t u r a space d a space c a s a over denominator m e d i d a space d a space s om br r end of fraction tan space 45 º equals a over 23 1 equals a over 23 a space equals space 23 space m$

Thus, the height of the house is 23 m.

question 4

A surveyor is a professional who uses mathematical and geometric knowledge to take measurements and study a surface. Using a theodolite, a tool that, among other functions, measures angles, positioned at 37 meters away from a building, he found an angle of 60° between a plane parallel to the ground and the height of the building. If the theodolite was on a tripod 180 cm from the ground, determine the height of the building in meters.

consider square root of 3 equals 1 point 73

see answer

Answer: The height of the building is 65.81 m.

Making a sketch of the situation we have:

Thus, the height of the building can be determined using the tangent of 60º, from the height where the theodolite is, adding the result with 180 cm or, 1.8 m, as it is the height it is from the ground.

The 60° tangent is equal to square root of 3 .

Height from the theodolite

$tan space 60 º space equals space numerator height space d the space p r is d i o over denominator 37 end of fraction square root of 3 space equals numerator space a l t u r a space d the space p r is d i o over denominator 37 end of fraction 1 comma 73 space. space 37 space equal to l t u r a space d o space p r is d i o 64 comma 01 space equal to space a l t u r a space d o space p r e d i o$

Total height

64.01 + 1.8 = 65.81 m

The height of the building is 65.81 m.

question 5

Determine the perimeter of the pentagon.

Consider:
sin 67° = 0.92
cos 67° = 0.39
tan 67° = 2.35

see answer

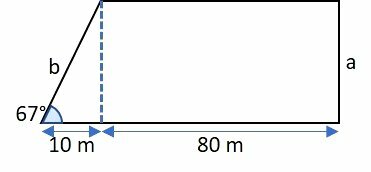
Answer: The perimeter is 219.1 m.

The perimeter is the sum of the sides of the pentagon. As there is a rectangular part measuring 80 m, the opposite side is also 80 m long.

The perimeter is given by:

P = 10 + 80 + 80 + a + b
P = 170 + a + b

Being The, parallel to the blue dashed line, we can determine its length using the 67° tangent.

tan space 67 degree sign equals a over 10 2 comma 35 space equals space a over 10 2 comma 35 space. space 10 space equals space a 23 comma 5 space equals space a

To determine the value of b, we use the cosine of 67°

$cos space 67 degree sign space equals space 10 over b b equals numerator 10 over denominator cos space 67 sign of degree end of fraction b equals numerator 10 over denominator 0 comma 39 end of fraction b space approximately equal 25 comma 6$

So the perimeter is:

P = 170 + 23.5 + 25.6 = 219.1 m

question 6

Find the sine and cosine of 1110°.

see answer

Considering the trigonometric circle we have that a complete turn has 360°.

When we divide 1110° by 360° we get 3.0833.... This means 3 full turns and a little more.

Taking 360° x 3 = 1080° and subtracting from 1110 we have:

1110° - 1080° = 30°

Considering the counterclockwise direction as positive, after three complete turns we return to the beginning, 1080° or 0°. From this point we advance another 30°.

So the sine and cosine of 1110° are equal to the sine and cosine of 30°

$s and n space 1110 degree sign space equals space s and n space 30 degree sign space equals space 1 half cos space 1110 sign of degree space equals space cos space 30 degree sign space equals space numerator square root of 2 over denominator 2 end of fraction$

question 7

(CEDERJ 2021) Studying for a trigonometry test, Júlia learned that sin² 72° is equal to

1 - cos² 72°.

cos² 72° - 1.

tg² 72° - 1.

1 - tg² 72º.

feedback explained

The fundamental relationship of trigonometry says that:

s and n squared x space plus space cos squared x equals 1

Where x is the value of the angle.

Taking x = 72º and isolating the sine, we have:

s and n squared space 72º equals 1 minus cos squared space 72º

question 8

Ramps are a good way to ensure accessibility for wheelchair users and people with reduced mobility. Accessibility to buildings, furniture, spaces and urban equipment is guaranteed by law.

The Brazilian Association of Technical Norms (ABNT), in accordance with the Brazilian Law for the Inclusion of Persons with Disability (13,146/2015), regulates the construction and defines the slope of the ramps, as well as the calculations for their construction. The ABNT calculation guidelines indicate a maximum slope limit of 8.33% (1:12 ratio). This means that a ramp, to overcome a difference of 1 m, must be at least 12 m long and this defines that the slope angle of the ramp, in relation to the horizontal plane, cannot be greater than 7°.

According to the previous information, so that a ramp, with a length equal to 14 m and an inclination of 7º in in relation to the plane, is within the ABNT norms, it must serve to overcome a gap with a maximum height of

Use: sin 7th = 0.12; cos 7º = 0.99 and tan 7º = 0.12.

a) 1.2 m.

b) 1.32 m.

c) 1.4 m.

d) 1.56 m.

e) 1.68 m.

feedback explained

The ramp forms a right triangle where the length is 14 m, making an angle of 7º in relation to the horizontal, where the height is the side opposite the angle.

Using sine of 7°:

s and n space 7 degree sign equal to a over 1414 space. s space and n space 7 degree sign space equals space a14 space. space 0 comma 12 space equals space a1 comma 68 space equals space a

s and n 7th space equals a over 140 point 12 space. space 14 space equals space a1 comma 68 space equals space a

The height that the ramp must reach is 1.68 m.

question 9

(Unesp 2012) A hospital building is being built on a sloping terrain. To optimize the construction, the responsible architect designed the parking lot in the basement of the building, with entrance from the back street of the land. The hospital's reception is 5 meters above the level of the parking lot, requiring the construction of a straight access ramp for patients with mobility difficulties. The figure schematically represents this ramp (r), connecting point A, on the reception floor, to point B, on the parking floor, which must have a minimum α inclination of 30º and a maximum of 45º.

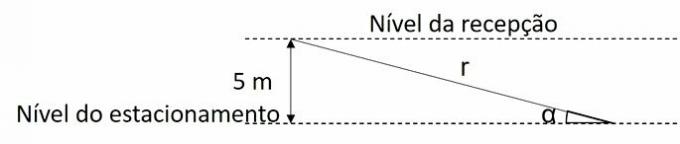
Under these conditions and considering square root of 2 equals 1 point 4 , what should be the maximum and minimum values, in meters, of the length of this access ramp?

see answer

Answer: The length of the access ramp will be 7 m minimum and 10 m maximum.

The project already foresees and sets the height at 5 m. We need to calculate the length of the ramp, which is the hypotenuse of the right triangle, for the angles of 30° and 45°.

For the calculation, we used the sine of the angle, being the ratio between the opposite side, 5m, and the hypotenuse r, which is the length of the ramp.

For the notable angles 30° and 45° the sine values are:

$s and n space 30 degree sign space equals space 1 half s and n space 45 degree sign space equals space numerator square root of 2 over denominator 2 end of fraction$

for 30°

$s and n space 30 degree sign equal to 5 over r r space equal to numerator 5 over denominator s and n degree 30 sign end of fraction r space equals numerator 5 over denominator start style show 1 middle end of style end of fraction r equals 5 space. space 2 r space equal to 10$

to 45°

$s and n space 45 degree sign equals 5 over r r equals numerator 5 over denominator s and n space 45 degree sign end of fraction r equals numerator 5 over denominator start style show numerator square root of 2 over denominator 2 end of fraction end of style end of fraction r equals numerator 5 space. space 2 over denominator square root of 2 end of fraction r space equal to numerator 10 over denominator square root of 2 end of fraction$

rationalizing

$r equals numerator 10 over denominator square root of 2 end of fraction. numerator square root of 2 over denominator square root of 2 end of fraction equals numerator 10 square root of 2 over denominator 2 end of fraction$

Substituting the value of

$r equals numerator 10 space. space 1 comma 4 over denominator 2 end of fraction equals 7$

question 10

(EPCAR 2020) At night, a Brazilian Air Force helicopter flies over a flat region and spots a UAV (Air Vehicle Unmanned) of circular shape and negligible height, with a radius of 3 m parked parallel to the ground at 30 m from height.

The UAV is at a distance y meters from a searchlight that has been installed on the helicopter.

The beam of light from the searchlight that passes the UAV falls on the flat region and produces a circular shadow with center O and radius R.

The radius R of the circle of the shadow forms an angle of 60º with the light beam, as seen in the following figure.

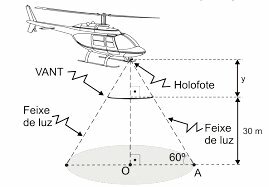
At that moment, a person who is at point A on the circumference of the shadow runs to point O, foot from the perpendicular drawn from the spotlight to the plane region.

The distance, in meters, that this person travels from A to O is a number between

a) 18 and 19

b) 19 and 20

c) 20 and 21

d) 22 and 23

feedback explained

objective

Determine the segment length AO in top frame , radius of the circle of the shadow.

Data

Height from O to UAV is 30 m.
The radius of the UAV is 3 m.

Using the 60° tangent we determine the part highlighted in red in the following image:

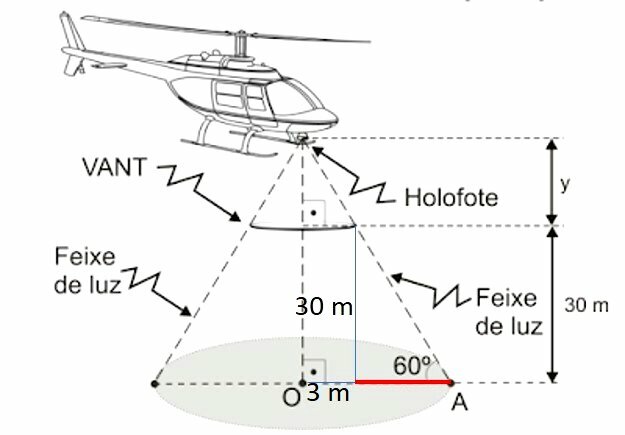
Image associated with the resolution of the issue.

Considering the tangent of 60° = square root of 3 and the tangent being the ratio between the side opposite the angle and its adjacent side, we have:

$tan space 60 degree sign equals 30 over xx equals numerator 30 over denominator square root of 3 end of fraction$

rationalizing

$x space equals space numerator 30 over denominator square root of 3 end of fraction. numerator square root of 3 over denominator square root of 3 end of fraction equals numerator 30 square root of 3 over denominator 3 end of fraction equals 10 square root of 3$