Study mode, mean and median with the solved and step-by-step exercises. Clear your doubts and prepare for exams and entrance exams.
Median Exercises
Exercise 1
In a pediatrics office, a doctor saw nine children in one day. He measured and noted the heights of the children as per the consultations.
| 1st consultation | 0.90 m |
|---|---|
| 2nd consultation | 1.30 m |
| 3rd consultation | 0.85 m |
| 4th consultation | 1.05 m |
| 5th consultation | 0.98 m |
| 6th consultation | 1.35 m |
| 7th consultation | 1.12 m |
| 8th consultation | 0.99 m |
| 9th consultation | 1.15 m |
Determine the median heights of children in consultations.
Correct answer: 1.05 m.
The median is a measure of central tendency. To determine the median we must organize the ROL of the data, which is to place them in ascending order.
| 0.85 m | 0.90 m | 0.98 m | 0.99 m | 1.05 m | 1.12 m | 1.15 m | 1.30 m | 1.35 m |
The median is the central value, in this case, the fifth value: 1.05 m.
Exercise 2
(Enem 2021) The manager of a concessionaire presented the following table at a meeting of directors. It is known that at the end of the meeting, in order to prepare goals and plans for the next year, the administrator will evaluate sales based on the median number of cars sold in the period from January to December.

What was the median of the data presented?
a) 40.0
b) 42.5
c) 45.0
d) 47.5
e) 50.0
Correct answer: b) 42.5
To determine the median, we need to organize the ROL of data, that is, put them in ascending order.

Since the number of elements is even, we must calculate the simple arithmetic mean between the two central values.
Therefore, 42.5 is the median of the data presented.
Exercise 3
(Enem 2015) In a selective for the final of the 100 meters freestyle swimming, in an Olympics, the athletes, in their respective lanes, obtained the following times:
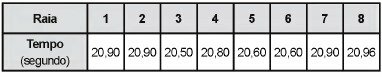
The median time shown in the table is
a) 20.70.
b) 20.77.
c) 20.80.
d) 20.85.
e) 20.90.
Correct answer: a) 20.70.
To determine the median we must assemble the ROL of data, arranging them in ascending order.

If the dataset is odd, the median is the central value. If the dataset number is even, the median will be the arithmetic mean between the central values.
Therefore, the median is 20.70.
Exercise 4
(UNEB 2013) Brazilians willing to pay a daily rate of up to €11 thousand (R$ 30.69 thousand) for a suite are the hot spot in the world's luxury hotel market.
Competing for the finest hotels, the clientele in Brazil occupies the third position in the ranking of reservations by The Leading Hotels of the World (LHW). The seal brings together some of the most sophisticated establishments in the world.
From 2010 to 2011, the local revenue of the light truck grew 16.26%.
Last year, the Brazilian office broke the record of US$ 31 million (R$ 66.96 million) in reserves.
(TOURIST..., 2012, p. B 3).
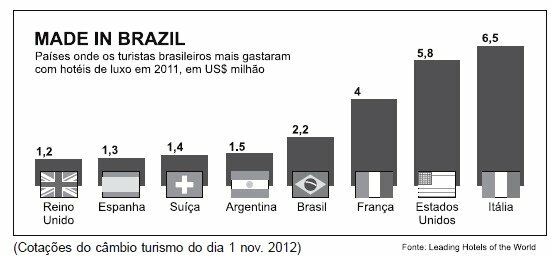
The median of spending, in millions of reais, of Brazilian tourists with luxury hotels, in 2011, is equal to
a) 3.764
b) 3,846
c) 3.888
d) 3,924
e) 3,996
Correct answer: e) 3,996
The median of the chart data is the arithmetic mean of the central values, in dollars.
The median is $1.85 million. However, the question asks for values in Reais.
The text states that US$ 31 million (of dollars) was equivalent to R$ 66.96 million (of reais).
We need to determine how many reais were worth one dollar. For this, we do the division:
Thus, 2.16 is the dollar-to-real conversion rate.
In real, Brazilians spent 3.996 million reais.
Average
Exercise 7
The following table shows prices for motorcycle taxi rides to different neighborhoods in the city of Rio de Janeiro and the amount of trips recorded in one day, for each neighborhood.
| neighborhoods | Price | Number of trips |
|---|---|---|
| Meier | BRL 20.00 | 3 |
| Mature | BRL 30.00 | 2 |
| Botafogo | BRL 35.00 | 3 |
| Copacabana | BRL 40.00 | 2 |
Calculate the average price of trips on that day.
Answer: BRL 27.00.
As each price has a different contribution to the average, as the amounts of trips are different for each neighborhood, the average has to be weighted by the amount of trips.
The weighted average is the division between each price multiplied by the respective amounts of trips and the total trips.
Thus, the average price of trips for that day was R$27.00.
Exercise 6
(Enem 2015) A contest consists of five stages. Each stage is worth 100 points. Each candidate's final score is the average of their grades over the five steps. The classification follows the descending order of the final scores. The tiebreaker is based on the highest score in the fifth stage.
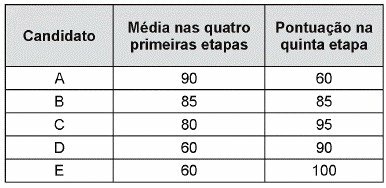
The final ranking order for this contest is
a) A, B, C, E, D.
b) B, A, C, E, D.
c) C, B, E, A, D.
d) C, B, E, D, A.
e) E, C, D, B, A.
Correct answer: b) B, A, C, E, D.
We need to determine the average of the five candidates.
We write e1 + e2 + e3 + e4 as the sum of the candidates' first four grades.
Candidate for
Thus,
Candidate A's five-step average
We've already determined the sum of the first four steps, which equals 360. From the table, we take the score of the fifth stage, 60.
Calculating the average, we have:
Candidate A's average scores in the first five stages were 84 points.
Repeating the reasoning for the other candidates, we have:
Candidate B:
In the first four stages,
In the five steps,
Candidate C:
In the first four stages,
In the five steps,
Candidate D:
In the first four stages,
In the five steps,
Candidate E:
In the first four stages,
In the five steps,
In descending order of scores, we have:
| B | 85 |
| THE | 84 |
| Ç | 83 |
| AND | 68 |
| D | 66 |
Exercise 7
(UFT 2013) The average height of the 35 adult Indians in a village is 1.65 m. Analyzing only the heights of the 20 men, the average is equal to 1.70 m. What is the average, in meters, of heights if we consider only women?
a) 1.46
b) 1.55
c) 1.58
d) 1.60
e) 1.65
Correct answer: c) 1.58
There are 35 people in the village, 20 of whom are men, 15 are women.
35 = 20 + 15
Average height of women.
Calling Sm the sum of women's heights, we have:
Soon,
Where x is the mean of women's heights.
Average height of men.
Where Sh is the sum of men's heights.
Average of all people in the village
Calling S, the sum of the heights of all the people in the village, this is the sum of the heights of men plus women.
Averaging the entire village, we have:
Substituting the values of Sh and Sm, we have:
Solving the equation for x,
if we consider only women, 1.58 m is the average height.
Exercises 8
(EsSA 2012) The arithmetic mean of all candidates in a competition was 9.0, of the selected candidates it was 9.8 and the eliminated ones was 7.8. What percentage of candidates are selected?
a) 20%
b) 25%
c) 30%
d) 50%
e) 60%
Correct answer: e) 60%
1st step: determine the percentage ratio of the selected
We must determine the ratio of those selected to the total number of candidates.
Where S is the number of selected candidates and T is the total number of candidates.
However, the number T of the total number of candidates is equal to the sum of those selected plus those eliminated.
T = S + E
Where E is the total eliminated.
Thus, the reason we must determine is:
2nd step: determine a relationship between S and E
We have that the total average was 9. In this way,
Where nT is the sum of all grades. This sum is the addition of the grades of the selected nS, plus the grades of the eliminated, nE.
nT = nS + nE
Then,
(equation I)
Also, we have to:
therefore,
and
therefore,
Substituting in equation I, we have:
Writing S in function of E:
3rd step: replace in the reason
the reason is
Replacing S,
4th step: transform into percentage
To turn it into a percentage, we multiply by 100
0.6 x 100 = 60%
Therefore, 60% is the percentage of selected candidates.
Fashion
Exercise 9
In a movie theater, popcorn is sold in packs of three sizes. After entering a session, the management carried out a survey to find out which of the packages was the most sold.
In order of sales, these were the values noted by the popcorn cashier.
20,30
17,50
17,50
17,50
20,30
20,30
11,40
11,40
17,50
17,50
11,40
20,30
Based on the fashion of the values, determine which size of popcorn was the best seller.
Right answer:
Fashion is the most repeated element. Each element repeated itself:
11.40 three times
17.50 x five times
20.30 x four times
Thus, the average popcorn was the most sold, as 17.50 is the most repeated value.
Exercise 10
(Navy 2014) Review the chart below.
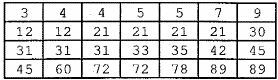
Check the option that shows the data mode in the table above.
a) 9
b) 21
c) 30
d) 30.5
e) 31
Correct answer: b) 21
Fashion is the most repeated element. Element 21 repeats 4 times.
Exercise 11
(Enem 2016) When starting its activities, an elevator operator records both the number of people that enter as the number of people leaving the elevator on each floor of the building where it works. The painting shows the records of the elevator operator during the first climb from the ground floor, where he and three other people depart, to the fifth floor of the building.

Based on the chart, what is the fashion for the number of people in the elevator going up from the ground floor to the fifth floor?
a) 2
b) 3
c) 4
d) 5
e) 6
Correct answer: d) 5.
We must consider the number of people entering, the number leaving and the number of people remaining.
| entered | went out | remain for walking | |
|---|---|---|---|
| 5th floor | 7 already had + 2 | 6 | 7 + 2 - 6 = 3 |
| 4th floor | 5 already had + 2 | 0 | 5 + 2 = 7 |
| 3rd floor | 5 already had + 2 | 2 | 5 + 2 - 2 = 5 |
| 2nd floor | 5 already had + 1 | 1 | 5 + 1 - 1 = 5 |
| 1 ° floor | 4 already had + 4 | 3 | 4 + 4 - 3 = 5 |
| Ground floor | 4 | 0 | 4 - 0 = 4 |
Thus, the fashion is 5, as it is the number of people that repeats the most.
Exercise 12
(UPE 2021) In the summer of 2018, a large appliance store recorded the number of fan units sold for 10 consecutive days, as shown in the table below. With this, it was possible to verify the sales volume per day and the variation in the number of sales from one day to the next.

What is the mode of variations in the number of daily sales in the period considered?
a) 53
b) 15
c) 7
d) 4
e) 2
Correct answer: d) 4.
The variation in the number of sales is the difference between one day and the previous one.
| Day 2 - Day 1 | 53 - 46 | 7 |
| Day 3 - Day 2 | 38 - 53 | - 15 |
| Day 4 - Day 3 | 45 - 38 | 7 |
| Day 5 - Day 4 | 49 - 45 | 4 |
| Day 6 - Day 5 | 53 - 49 | 4 |
| Day 7 - Day 6 | 47 - 53 | -6 |
| Day 8 - Day 7 | 47 - 47 | 0 |
| Day 9 - Day 8 | 51 - 47 | 4 |
| Day 10 - Day 9 | 53 - 51 | 2 |
With 4 being the most repeated difference, 4 is fashion.
learn more about Average, Fashion and Median.
You may be interested in:
- Arithmetic Average Exercises
- Arithmetic average
- Weighted Arithmetic Average
- Statistics - Exercises
- Statistic
- Geometric Mean
- Relative Frequency
- Standard deviation
- Dispersion Measures
- Variance and standard deviation


