The equation of the line can be determined by plotting it on the Cartesian plane (x, y). Knowing the coordinates of two distinct points belonging to the line we can determine its equation.
It is also possible to define an equation of the straight line based on its inclination and the coordinates of a point that belongs to it.
general equation of the line
Two points define a line. In this way, we can find the general equation of the line by aligning two points with a generic point (x, y) on the line.
Let the points A(xTheyyThe) and B(xByyB), non-coincident and belonging to the Cartesian plan.
Three points are aligned when the determinant of the matrix associated with those points is equal to zero. So we must calculate the determinant of the following matrix:
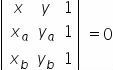
Developing the determinant we find the following equation:
(yThe -yB) x + (xB - xThe) y + xTheyB - xByThe = 0
Let's call:
a = (yThe -yB)
b = (xB - xThe)
c = xTheyB - xByThe
The general equation of the straight line is defined as:
ax + by + c = 0
Where The, B and ç are constant and The and B they cannot be simultaneously null.
Example
Find a general equation of the line that passes through the points A(-1, 8) and B(-5, -1).
First we must write the three-point alignment condition, defining the matrix associated with the given points and a generic point P(x, y) belonging to the line.
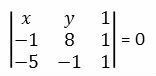
Developing the determinant, we find:
(8+1)x + (1-5)y + 40 + 1 = 0
The general equation of the line passing through points A(-1,8) and B(-5,-1) is:
9x - 4y + 41 = 0
To learn more, read also:
- Headquarters
- determinant
- Laplace's Theorem
Line reduced equation
Angular coefficient
We can find an equation of the line r knowing its inclination (direction), that is, the value of the angle θ that the line presents in relation to the x axis.
For this we associate a number m, which is called the slope of the line, such that:
m = tg θ
the slope m it can also be found by knowing two points belonging to the straight line.

As m = tg θ, then:
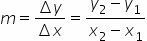
Example
Determine the slope of the line r, which passes through points A(1,4) and B(2,3).
Being,
x1 = 1 and y1 = 4
x2 = 2 and y2 = 3

Knowing the angular coefficient of the line m and a point P0(x0yy0) belonging to it, we can define its equation.
For this, we will substitute the known point P in the slope formula.0 and a generic point P(x, y), also belonging to the line:
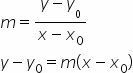
Example
Determine an equation of the line that passes through point A(2,4) and has slope 3.
To find the equation of the line, just replace the given values:
y - 4 = 3 (x - 2)
y - 4 = 3x - 6
-3x + y + 2 = 0
linear coefficient
the linear coefficient no straight r is defined as the point where the line intersects the y axis, that is, the point of coordinates P(0,n).
Using this point, we have:
y - n = m (x - 0)
y = mx + n (Reduced line equation).
Example
Knowing that the equation of the line r is given by y = x + 5, identify its slope, its slope, and the point where the line intersects the y axis.
As we have the reduced equation of the line, then:
m = 1
Where m = tg θ ⇒ tg θ = 1 ⇒ θ = 45º
The point of intersection of the line with the y axis is the point P(0,n), where n=5, then the point will be P(0.5)
Read too Calculation of slope
Line segment equation
We can calculate the slope using the point A(a, 0) that the line intersects the x-axis and the point B(0,b) that intersects the y-axis:
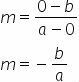
Considering n = b and substituting in reduced form, we have:
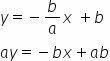
Dividing all members by ab, we find the segmentary equation of the line:
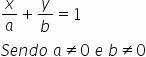
Example
Write, in segmentary form, the equation of the line that passes through point A(5.0) and has slope 2.
First let's find the point B(0,b), substituting in the slope expression:
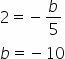
Substituting the values in the equation, we have the segmentary equation of the line:

Also read about:
- Cartesian Plan
- Distance between two points
- conical
- straight
- Parallel Lines
- Perpendicular Lines
- Line Segment
- Linear Function
- Affine Function
- Related Function Exercises
Solved Exercises
1) Given the line that has the equation 2x + 4y = 9, determine its slope.
4y = - 2x + 9
y = - 2/4 x + 9/4
y = - 1/2 x + 9/4
Therefore m = - 1/2
2) Write the equation of the line 3x + 9y - 36 = 0 in reduced form.
y = -1/3 x + 4
3) ENEM - 2016
For a science fair, two rocket projectiles, A and B, are being built to be launched. The plan is for them to be launched together, with the aim of projectile B intercepting A when it reaches its maximum height. For this to happen, one of the projectiles will describe a parabolic trajectory, while the other will describe a supposedly straight trajectory. The graph shows the heights reached by these projectiles as a function of time, in the simulations carried out.
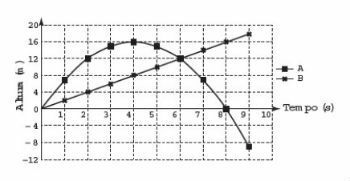
Based on these simulations, it was observed that the trajectory of projectile B should be changed so that the
objective was achieved.
To reach the goal, the angular coefficient of the line that represents the trajectory of B must
a) decrease by 2 units.
b) decrease by 4 units.
c) increase by 2 units.
d) increase by 4 units.
e) increase by 8 units.
First we must find the initial value of the slope of line B.
Remembering that m = tg Ɵ, we have:
m1 = 12/6 = 2
To pass through the maximum height point of the trajectory of A, the slope of the line B must have the following value:
m2 = 16/4 = 4
Thus, the slope of the line B will have to change from 2 to 4, then it will increase by 2 units.
Alternative c: increase 2 units
See too: Exercises on Analytical Geometry