O Pythagorean theorem lists the length of the sides of the right triangle. This geometric figure is formed by an internal angle of 90°, called a right angle.
The statement of this theorem is:
"The sum of the squares of your legs corresponds to the square of your hypotenuse."
Pythagoras theorem formula
According to the statement of the Pythagorean Theorem, the formula is represented as follows:
The2 = b2 + c2
Being,
The: hypotenuse
B: cateto
ç: cateto
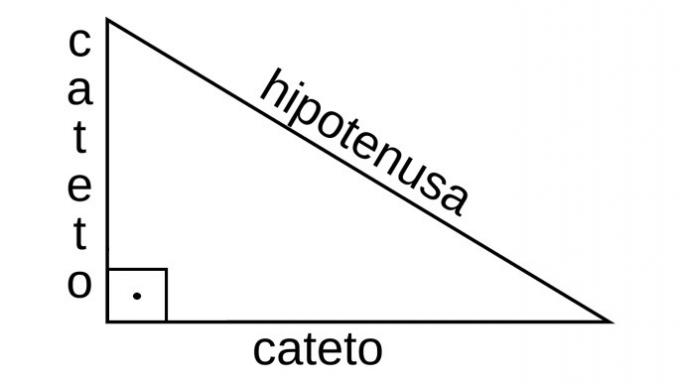
THE hypotenuse is the longest side of a right triangle and the side opposite the right angle. The other two sides are the legs. The angle formed by these two sides has a measure equal to 90º (right angle).
We also identified the legs, according to a reference angle. That is, the side can be called adjacent side or opposite side.
When the leg is close to the reference angle, it is called adjacent, on the other hand, if it is against this angle, it is called opposite.

Below are three examples of applications of the Pythagorean theorem to the metric relationships of a right triangle.
Example 1: calculate the measure of the hypotenuse
If a right triangle has 3 cm and 4 cm as measures of the legs, what is the hypotenuse of this triangle?
Therefore, the sides of the right triangle are 3 cm, 4 cm and 5 cm.
Example 2: calculate the measure of one of the legs
Determine the measure of a leg that is part of a right triangle, whose hypotenuse is 20 cm and the other leg measures 16 cm.
Therefore, the measurements of the sides of the right triangle are 12 cm, 16 cm and 20 cm.
Example 3: check whether a triangle is a rectangle
A triangle has sides measuring 5 cm, 12 cm and 13 cm. How do you know if it's a right triangle?
To prove that a right triangle is true, the measurements of its sides must obey the Pythagorean Theorem.
As the measures given satisfy Pythagoras' theorem, ie, the square of the hypotenuse is equal to the sum of the square of the legs, then we can say that the triangle is a rectangle.
Read too: Metric Relations in the Rectangle Triangle
Pythagorean Triangle
When measures the sides of a right triangle are positive integers, the triangle is called a Pythagorean triangle.
In this case, the legs and the hypotenuse are called “Pythagorean suit” or “Pythagorean trio”. To check whether three numbers form a Pythagorean trio, we use the relation to2 = b2 + c2.
The best known Pythagorean trio is represented by the numbers: 3, 4, 5. The hypotenuse being equal to 5, the greater leg equal to 4 and the smaller leg equal to 3.

Note that the area of the squares drawn on each side of the triangle are related just like the Pythagoras' theorem: the area of the square on the long side corresponds to the sum of the areas of the other two square.
Interestingly, the multiples of these numbers also form a Pythagorean suit. For example, if we multiply the trio 3, 4 and 5 by 3, we get the numbers 9, 12 and 15 which also form a Pythagorean suit.
In addition to suit 3, 4 and 5, there are a multitude of other suits. As an example, we can mention:
- 5, 12 and 13
- 7, 24, 25
- 20, 21 and 29
- 12, 35 and 37
Read too: Trigonometry in the Rectangle Triangle
Who was Pythagoras?
according to history Pythagoras of Samos (570 a. Ç. - 495 a. C.) was a Greek philosopher and mathematician who founded the Pythagorean School, located in southern Italy. Also called the Pythagorean Society, it included studies in Mathematics, Astronomy and Music.
Although the metric relationships of the right triangle were already known by the Babylonians, who lived long before Pythagoras, the first proof that this theorem applied to any right triangle is believed to have been made by Pythagoras.
The Pythagorean Theorem is one of the best known, most important and used theorems in mathematics. It is essential in solving problems in analytic geometry, plane geometry, spatial geometry and trigonometry.
In addition to the theorem, other important contributions of the Pythagorean Society for Mathematics were:
- Discovery of irrational numbers;
- Properties of integers;
- MMC and MDC.
Read too: Math Formulas
Proofs of the Pythagorean Theorem
There are several ways to prove Pythagoras' theorem. For example, the book The Pythagorean Proposition, published in 1927, presented 230 ways to demonstrate it, and another edition, released in 1940, increased to 370 demonstrations.
Watch the video below and check out some demonstrations of the Pythagorean Theorem.
Commented Exercises on the Pythagorean Theorem
question 1
(PUC) The sum of the squares of the three sides of a right triangle equals 32. How long is the hypotenuse of the triangle?
a) 3
b) 4
c) 5
d) 6
Correct alternative: b) 4.
From the information in the statement, we know that the2 + b2 + c2 = 32. On the other hand, by the Pythagoras theorem we have to2 = b2 + c2 .
Replacing the value of b2+c2 by the2 in the first expression, we find:
The2 + the2 =32 ⇒ 2. The2 = 32 ⇒ to2 = 32/2 ⇒ to2 = 16 ⇒ a = √ 16
a=4
For more questions, see: Pythagoras Theorem - Exercises
question 2
(And either)

In the figure above, which represents the design of a staircase with 5 steps of the same height, the total length of the handrail is equal to:
a) 1.9m
b) 2.1m
c) 2.0m
d) 1.8m
e) 2.2m
Correct alternative: b) 2.1m.
The total length of the handrail will be equal to the sum of the two stretches of length equal to 30 cm with the stretch that we do not know the measure for.
We can observe from the figure that the unknown section represents the hypotenuse of a right triangle, whose measure of one of the legs is equal to 90 cm.
To find the measure of the other leg, we must add the length of the 5 steps. Therefore, we have b = 5. 24 = 120 cm.
To calculate the hypotenuse, let's apply Pythagoras' theorem to this triangle.
The2 = 902 + 1202 to2 = 8100 + 14 400 ⇒ to2 = 22 500 ⇒ a = √ 22 500 = 150 cm
Note that we could have used the idea of the Pythagorean suits to calculate the hypotenuse, since the legs (90 and 120) are multiples of the 3, 4, and 5 suit (multiplying all terms by 30).
In this way, the total measure of the handrail will be:
30 + 30 + 150 = 210 cm = 2.1 m
Test your knowledge with Trigonometry Exercises
question 3
(UERJ) Millôr Fernandes, in a beautiful tribute to Mathematics, wrote a poem from which we extract the fragment below:
To so many sheets of a Mathematics book,
a Quotient fell in love one day wildly
by an Unknown.
He looked at her with his innumerable gaze
and he saw her from apex to base: an odd figure;
rhomboid eyes, trapezoid mouth,
rectangular body, spheroid breasts.
He made your life parallel to hers,
until they met in Infinity.
"Who are you?" - He asked in radical anxiety.
“I am the sum of the squares of the legs.
But you can call me hypotenuse.”
(Millôr Fernandes. Thirty Years of Myself.)
Incognita was wrong to say who it was. To meet the Pythagoras Theorem, the following should be done
a) “I am the square of the sum of the legs. But call me the hypotenuse square.”
b) “I am the sum of the legs. But you can call me hypotenuse.”
c) “I am the square of the sum of the legs. But you can call me hypotenuse.”
d) “I am the sum of the squares of the legs. But call me the hypotenuse square.”
Alternative d) “I am the sum of the squares of the legs. But call me the hypotenuse square.”
Learn more about the topic:
- isosceles triangle
- Sine, Cosine and Tangent
- Mathematics in Enem