THE elastic force and the force reaction of elastic materials, which is contrary to the external force that compresses or stretches it. The formula for the elastic force is stated by Hooke's law, which relates the force to the spring deformation. Thus, we can find its value through the product of the deformation suffered by the elastic constant of the material.
Know more: Weight force — the gravitational force produced by a second massive body
Topics in this article
- 1 - Summary about elastic force
-
2 - What is elastic force?
- Hooke's Law Video
-
3 - What is the formula for elastic force?
- Elastic constant
- 4 - Work of the elastic force
- 5 - How to calculate the elastic force?
- 6 - Exercises solved on elastic force
Tensile strength summary
The elastic force determines the deformation suffered by the spring.
Its calculation is done using Hooke's law.
Hooke's law states that the force is proportional to the deformation of the spring.
Hooke's law first appeared in the form of anagram “ceiiinosssttuv”, which stands for “ut tensio, sic vis” and means: “As deformation, so force.”
The elastic constant deals with the ease or difficulty in deforming the spring and is defined by the dimensions and nature of the elastic material.
The work of the spring force is determined by the product of the spring constant and the square of the spring strain, all divided by two.
Both the elastic force formula and its job have a negative sign, which represents the tendency of the force to be opposite to the motion of the spring.
Do not stop now... There's more after the ad ;)
What is elastic force?
The elastic force is the force associated with deformation of the spring or other materials, such as rubbers and rubber bands. It acts in the opposite direction to the force received by the body. That is, if we push the spring aiming at its compression, it will do the same force, but in the opposite direction, aiming at its decompression.
Its calculation is made using Hooke's law, enunciated in 1678 by Robert Hooke (1635–1703) in the form of the anagram “ceiiinosssttuv”, in order to reserve its information to itself. Only after two years did he decipher it as “ut tensio, sic vis”, which means “as deformation, so force”, representing the relationship of proportionality existing between force and deformation.
→ Hooke's Law Video
What is the formula for elastic force?
The elastic force formula, that is, Hooke's law, is expressed by:
\(F_{el}=-\ k\bullet∆x\)
On what:
\(∆x=xf-xi\)
\(Gall}\): the elastic force, that is, the force exerted by the spring, measured in Newtons \([N]\).
k: the spring constant, measured in [\(N/m\)].
\(∆x\): the change in spring deformation (also called elongation), measured in meters [\(m\)].
\(x_i\): the initial length of the spring, measured in meters [\(m\)].
\(x_f\): the final length of the spring, measured in meters [\(m\)].
Important: The negative sign in the formula exists because the force tends to oppose the displacement of the body, aiming at the equilibrium of the system, as in figure 2 below.
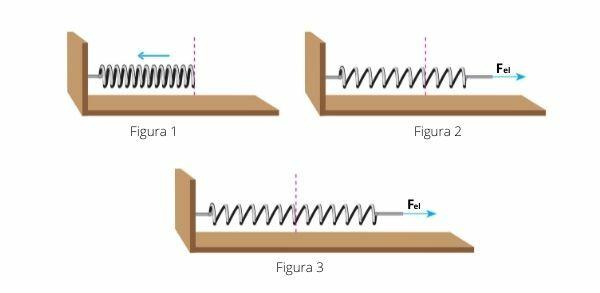
However, if \(F_{el}>0\) for \(x<0\), as in figure 1, there is compression of the spring. Already is \(F_{el}<0\) for \(x>0\), as in figure 3, the spring is stretched.
→ Elastic constant
The spring constant determines the stiffness of the spring, that is, how much force is necessary for the spring to deform. Its value depends exclusively on the nature of the material in which it was made and its dimensions. Therefore, the greater the spring constant, the more difficult it is to deform.

elastic force work
Every force does work. So, the strength work elastic is found using the formula:
\(W_{el}=-\left(\frac{{k\bullet x_f}^2}{2}-\frac{{k\bullet x_i}^2}{2}\right)\)
Suposing that xi=0 and calling xf in x, we have its best known form:
\(W_{el}=-\frac{{k\bullet x}^2}{2}\)
\(W_{el}\): the work of the elastic force, measured in Joules [J].
k: the spring constant, measured in [No/m].
\(x_i\): the initial length of the spring, measured in meters [m].
\(x_f\) or x: the final length of the spring, measured in meters [m].
Read too: Tensile force — the force applied to ropes or wires
How to calculate the elastic force?
From a mathematical point of view, the elastic force is calculated through its formula and whenever we are working with springs. Below we will see an example of how to calculate the spring force.
Example:
Knowing that the spring constant of a spring is equal to 350 N/m, determine the force required to deform the spring by 2.0 cm.
Resolution:
We will calculate the force required to deform the spring using Hooke's law:
\(F_{el}=k\bullet x\)
Transforming the strain of 2 cm into meters and substituting the value of the spring constant:
\(F_{el}=350\bullet0.02\)
\(F_{el}=7\ N\)
Exercises solved on elastic force
question 1
When compressed by a force of 10 N, a spring changes its length by 5 cm (0.05 m). The spring constant of this spring, in N/m, is about:
A) 6.4 N/m
B) 500 N/m
C) 250 N/m
D) 200 N/m
E) 12.8 N/m
Resolution:
Alternative D
We will do the calculation using Hooke's law:
\(F_{el}=k\bullet x\)
\(10=k\bullet0.05\)
\(k=\frac{10}{0.05}\)
\(k=200\ N/m\)
question 2
A spring of spring constant of 500 N/m is pressed by a force of 50 N. Based on this information, calculate what is, in centimeters, the deformation suffered by the spring due to the application of this force.
A) 100
B) 15
C)0.1
D) 1000
E) 10
Resolution:
Alternative E
We will calculate the deformation of the spring using Hooke's law:
\(F_{el}=k\bullet x\)
\(50=500\bullet x\)
\(x=\frac{50}{500}\)
\(x=0.1\ m\)
\(x=10\ cm\)
By Pâmella Raphaella Melo
Physics teacher
Would you like to reference this text in a school or academic work? Look:
MELO, Pâmella Raphaella. "elastic force"; Brazil School. Available in: https://brasilescola.uol.com.br/fisica/forca-elastica.htm. Accessed on April 27, 2022.


