THE law of sins determines that in any triangle, the sine relation of an angle is always proportional to the measure of the side opposite that angle.
This theorem demonstrates that in the same triangle the ratio between the value of one side and the sine of its opposite angle will always be constant.
Thus, for a triangle ABC with sides a, b, c, the Law of Sins admits the following relations:
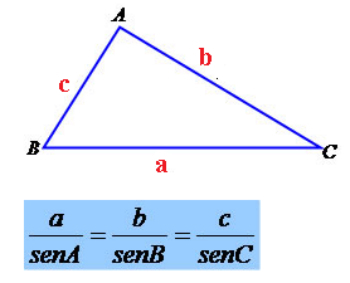
Representation of the Laws of Sins in the triangle
Example
For a better understanding, let's calculate the measure of sides AB and BC of this triangle, as a function of measure b of side AC.
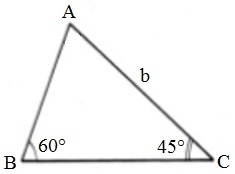
By the law of sines, we can establish the following relationship:

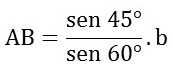
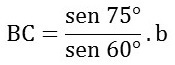
Hence, AB = 0.816b and BC = 1.115b.
Note: The values of sines were consulted in table of trigonometric ratios. In it, we can find the values of the angles from 1º to 90º of each trigonometric function (sine, cosine and tangent).
The angles of 30º, 45º and 60º are most used in trigonometry calculations. Hence, they are called remarkable angles. Check out a table with the values below:
| Trigonometric Relations | 30° | 45° | 60° |
|---|---|---|---|
| Sine | 1/2 | √2/2 | √3/2 |
| cosine | √3/2 | √2/2 | 1/2 |
| Tangent | √3/3 | 1 | √3 |
Application of the Law of Sins
We use the Sine Law in acute triangles, where the internal angles are less than 90º (acute); or in obtuse triangles, which have internal angles greater than 90º (obtuse). In these cases, you can also use the Cosine Law.
The main objective of using the Law of Sins or Cosines is to discover the measurements of the sides of a triangle and also its angles.

Representation of triangles according to their internal angles
And the Law of Sins in the Rectangle Triangle?
As mentioned above, the Law of Sins is used in both acute and obtuse triangles.
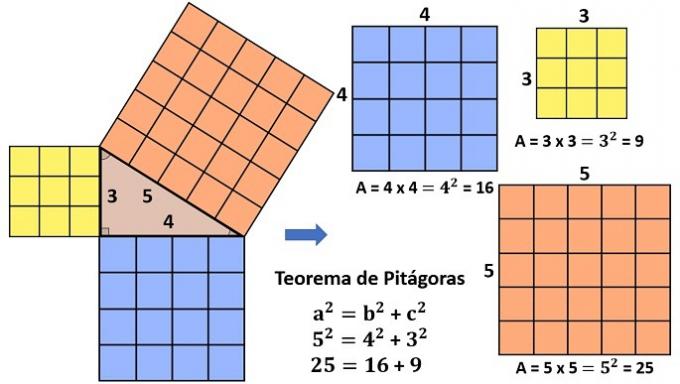
In the right triangles, formed by an internal angle of 90º (straight), we used the Pythagorean Theorem and the relations between its sides: opposite, adjacent side and hypotenuse.
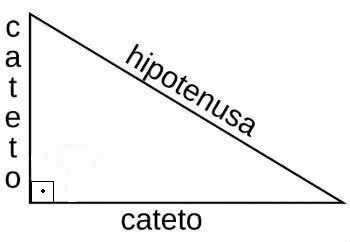
Representation of the right triangle and its sides
This theorem has the following statement: "the sum of the squares of their legs corresponds to the square of their hypotenuse". Its formula is expressed:
H2 = ca2 + co2
Thus, when we have a right triangle, the sine will be the ratio between the length of the opposite leg and the length of the hypotenuse:
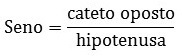
It reads opposite on the hypotenuse.
The cosine corresponds to the proportion between the length of the adjacent leg and the length of the hypotenuse, represented by the expression:
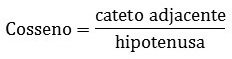
It is read adjacent to the hypotenuse.
Entrance Exam Exercises
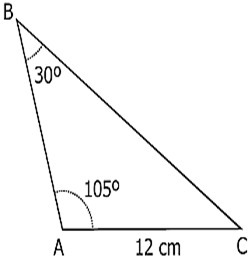
1.(UFPB) The city hall of a certain city will build, over a river that crosses that city, a bridge that must be straight and connect two points, A and B, located on the opposite banks of the river. To measure the distance between these points, a surveyor located a third point, C, 200 m away from point A and on the same bank of the river as point A. Using a theodolite (a precision instrument for measuring horizontal angles and vertical angles, often used in topographic work), the surveyor observed that the angles measured, respectively, 30º and 105º, as illustrated in the following figure.

Based on this information, it is correct to state that the distance, in meters, from point A to point B is:
objective: Determine the measure of AB.
Idea 1 - Law of Sins to determine AB
The figure forms triangle ABC, where the side AC measures 200 m and we have two determined angles.
being the angle opposite the side AC of 200 m and the angle C opposite the side AB, we can determine AB through the sins law.
THE sins law determines that the ratios between the measurements of the sides and the sines of the opposite angles, respective to these sides, are equal in the same triangle.
Idea 2 - determine the angle
The sum of the interior angles of a triangle is 180°, so we can determine angle B.
B + 105° + 30° = 180°
B = 180° - 105° - 30°
B = 45°
Replacing the value of in the law of sines and making the calculations.
Note that there is a square root in a denominator. Let's take this root by doing the rationalization, which is the multiplication of both the denominator and numerator of the fraction by the root itself.
Replacing the AC value, we have:
Therefore, the distance between points A and B is .
2. (Mackenzie – SP) Three islands A, B and C appear on a map in 1:10000 scale, as shown in the figure. Of the alternatives, the one that best approximates the distance between islands A and B is:
a) 2.3 km
b) 2.1 km
c) 1.9 km
d) 1.4 km
e) 1.7 km
Correct answer: e) 1.7 km
Purpose: To determine the measure of segment AB.
Idea 1: Use the sine law to find the measure of AB
Law of Sins: The measurements of the sides of a triangle are proportional to the sines of their opposite angles.
Idea 2: determine the angle
The sum of the interior angles of a triangle equals 180º.
30 + 105 + C = 180
135 + C = 180
C = 180 - 135
C = 45
Idea 3: Apply the value of C in the law of sines
Idea 4: approximate the square root value and use the scale
Making
12. 1,4 = 16,8
The scale says 1:10000, multiplying:
16,8. 10000 = 168 000 cm
Idea 5: moving from cm to km
168 000 cm / 100 000 = 1.68 km
Conclusion: As the calculated distance is 1.68 km, the closest alternative is the letter e.
Note: To go from cm to km, we divide by 100 000 because, on the following scale, from centimeters to km, we count 5 places to the left.
km -5- hm -4- dam -3- m -2- dm -1- cm mm
3. (Unifor-CE) It is known that in every triangle the measure of each side is directly proportional to the sine of the angle opposite to the side. Using this information, it is concluded that the measure of side AB of the triangle shown below is:
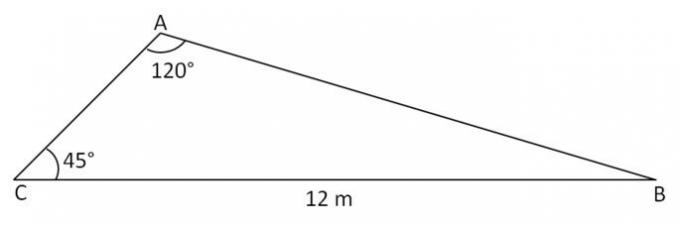
The statement provides the law of sines.
From trigonometry, we have that: sin 120 = sin 60.
Replacing the values in the formula:
In order not to leave a root in the denominator, we use rationalization, multiplying the denominator and the numerator by the root of 3.
Therefore, the measure on the AB side is .
Read more about the topic:
- Sine, Cosine and Tangent
- Trigonometry
- Trigonometric Relations
- Trigonometric Circle
- Trigonometric Functions
- Trigonometric Ratios