THE trigonometry in the right triangle is the study of triangles that have an internal angle of 90°, called a right angle.
Remember that trigonometry is the science responsible for the relationships established between triangles. They are flat geometric figures composed of three sides and three internal angles.
The triangle called equilateral has sides with equal measures. The isosceles has two sides with equal measurements. The scalene, on the other hand, has three sides with different measurements.
With respect to the angles of triangles, interior angles greater than 90° are called obtuse angles. On the other hand, internal angles smaller than 90° are called acutangles.
Also, the sum of the interior angles of a triangle will always be 180°.
Rectangle Triangle Composition
The right triangle is formed:
- Catets: are the sides of the triangle that form the right angle. They are classified into: adjacent side and opposite side.
- Hypotenuse: is the side opposite the right angle, being considered the longest side of the right triangle.
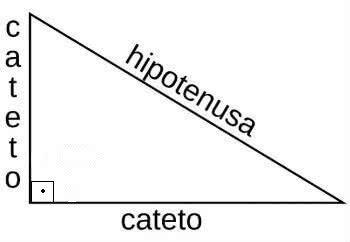
According to the Pythagorean theorem, the sum of the squares of the legs of a right triangle is equal to the square of its hypotenuse:
H2 = ca2 + co2
Read too:
- Trigonometry
- angles
- Rectangle Triangle
- Triangle Classification
Trigonometric Relations of the Rectangle Triangle
Trigonometric ratios are the relationships between the sides of a right triangle. The main ones are the sine, cosine and tangent.
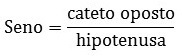
It reads opposite on the hypotenuse.
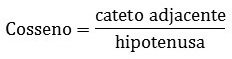
It is read adjacent to the hypotenuse.
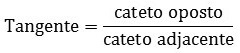
It reads opposite side over adjacent side.
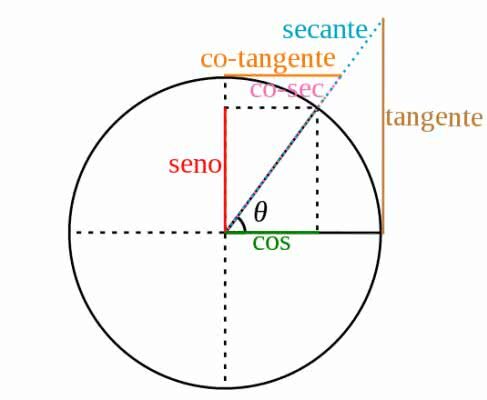
Trigonometric circle and trigonometric ratios
The trigonometric circle is used to help with trigonometric relationships. Above, we can find the main reasons, where the vertical axis corresponds to sine and the horizontal axis to cosine. Besides them, we have the inverse reasons: secant, cosecant and cotangent.

One reads about the cosine.
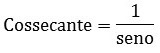
One reads about the sine.
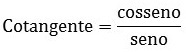
It reads cosine over sine.
Read too:
- Sine, Cosine and Tangent
- Trigonometric Circle
- Trigonometric Functions
- Trigonometric Ratios
- Metric Relations in the Rectangle Triangle
Remarkable Angles
the calls angles remarkable are those that appear most often, namely:
| Trigonometric Relations | 30° | 45° | 60° |
|---|---|---|---|
| Sine | 1/2 | √2/2 | √3/2 |
| cosine | √3/2 | √2/2 | 1/2 |
| Tangent | √3/3 | 1 | √3 |
know more:
- Trigonometry Exercises in the Right Triangle
- Trigonometry Exercises
- law of sins
- Cosine Law
- Trigonometric Relations
- Trigonometric Table
Exercise solved
In a right triangle, the hypotenuse measures 8 cm and one of the internal angles is 30°. What is the value of the opposite (x) and adjacent (y) sides of this triangle?
According to trigonometric relationships, sine is represented by the following relationship:
Sen = opposite leg/hypotenuse
Sen 30° = x/8
½ = x/8
2x = 8
x = 8/2
x = 4
Soon, the opposite leg of this right triangle measures 4 cm.
From this, if the square of the hypotenuse is the sum of the squares of its legs, we have:
Hypotenuse2 = opposite side2 + adjacent cateto2
82 = 42+y2
82 - 42 = y2
64 - 16 = y2
y2 = 48
y = √48
Soon, the adjacent leg of this right triangle measures √48 cm.
Thus, we can conclude that the sides of this triangle measure 8 cm, 4 cm and √48 cm. Its internal angles are 30° (sharp), 90° (straight) and 60° (sharp angle), since the sum of the internal angles of the triangles will always be 180°.
Entrance Exam Exercises
1. (Vunesp) The cosine of the smallest internal angle of a right triangle is √3/2. If the measure of the hypotenuse of this triangle is 4 units, then it is true that one of the legs of this triangle measures, in the same unit,
to 1
b) √3
c) 2
d) 3
e) √3/3
Alternative c) 2
2. (FGV) In the following figure, segment BD is perpendicular to segment AC.

If AB = 100m, an approximate value for the DC segment is:
a) 76m.
b) 62m.
c) 68m.
d) 82m.
e) 90m.
Alternative d) 82m.
3. (FGV) A theater audience, viewed from above, occupies the ABCD rectangle in the figure below, and the stage is adjacent to the BC side. The rectangle measurements are AB = 15m and BC = 20m.
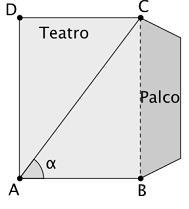
A photographer who will be in corner A of the audience wants to photograph the entire stage and, for that, must know the angle of the figure in order to choose the proper aperture lens.
The cosine of the angle in the figure above is:
a) 0.5
b) 0.6
c) 0.75
d) 0.8
e) 1.33
Alternative b) 0.6
4. (Unoesc) A man of 1.80 m stands 2.5 m away from a tree, as illustrated below. Knowing that the angle α is 42°, determine the height of this tree.
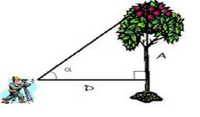
Use:
42° sine = 0.669
42° cosine = 0.743
42° tangent = 0.90
a) 2.50 m.
b) 3.47 m.
c) 3.65 m.
d) 4.05 m.
Alternative d) 4.05 m.
5. (Enem-2013) The towers Puerta de Europa they are two towers leaning against each other, built on an avenue in Madrid, Spain. The slope of the towers is 15° from the vertical and they are each 114 m high (the height is indicated in the figure as segment AB). These towers are a good example of an oblique square-based prism and one of them can be seen in the image.

Available in: www.flickr.com. Accessed on: 27 mar. 2012.
Using 0.26 as an approximate value for the 15° tangent and two decimal places in the operations, it is found that the base area of this building occupies a space on the avenue:
a) less than 100m2.
b) within 100 m2 and 300 m2.
c) between 300 m2 and 500 m2.
d) within 500 m2 and 700 m2.
e) greater than 700 m2.
Alternative e) greater than 700 m2.