Matrices: Commented and Solved Exercises

Matrix is ​​a table formed by real numbers, arranged in rows and columns. The numbers that appear in the matrix are called elements.

Take advantage of the solved and commented entrance exam questions to clear all your doubts regarding this content.

Entrance Exam Issues Resolved

1) Unicamp - 2018

Let a and b be real numbers such that the matrix A = satisfies equation A²= aA + bI, where I is the identity matrix of order 2. So the product ab is equal to

a) −2.
b) −1.
c) 1.
d) 2.

See Answer

To find out the value of product a.b, we first need to know the value of a and b. So let's consider the equation given in the problem.

To solve the equation, let's calculate the value of A², which is done by multiplying matrix A by itself, that is:

This operation is done by multiplying the rows of the first matrix by the columns of the second matrix, as shown below:

In this way the matrix A² it's the same as:

Considering the value we just found and remembering that in the identity matrix the elements of the main diagonal are equal to 1 and the other elements are equal to 0, the equation will be:

We now have to multiply the matrix A by the number a and the identity matrix by the number b.

Remember that to multiply a number by an array, we multiply the number by each element of the array.

Thus, our equality will be equal to:

Adding the two matrices, we have:

Two matrices are equal when all corresponding elements are equal. In this way, we can write the following system:

Isolating the a in the second equation:

Substituting the value found for a in the first equation, we find the value of b:

2 + b = 1
b = 1 - 2
b = -1

Thus, the product will be given by:

The. b = - 1. 2
The. b = - 2

Alternative: a) −2.

2) Unesp - 2016

A point P, of coordinates (x, y) of the orthogonal Cartesian plane, is represented by the column matrix. , as well as the column matrix represents, in the orthogonal Cartesian plane, the point P of coordinates (x, y). Thus, the result of matrix multiplication is a column matrix that, in the orthogonal Cartesian plane, necessarily represents a point that is

a) a 180º rotation of P in the clockwise direction, and with center at (0, 0).
b) a rotation of P through 90° counterclockwise, with center at (0, 0).
c) symmetric of P with respect to the horizontal x axis.
d) symmetric of P with respect to the vertical y axis.
e) a rotation of P through 90º clockwise, and with center at (0, 0).

See Answer

The point P is represented by a matrix, such that the abscissa (x) is indicated by the element a.₁₁ and the ordinate (y) by element a₂₁ of the matrix.

To find the new position of point P, we must solve the multiplication of the presented matrices and the result will be:

The result represents the new coordinate of point P, that is, the abscissa is equal to -y and the ordinate is equal to x.

To identify the transformation undergone by the position of point P, let's represent the situation in the Cartesian plane, as indicated below:

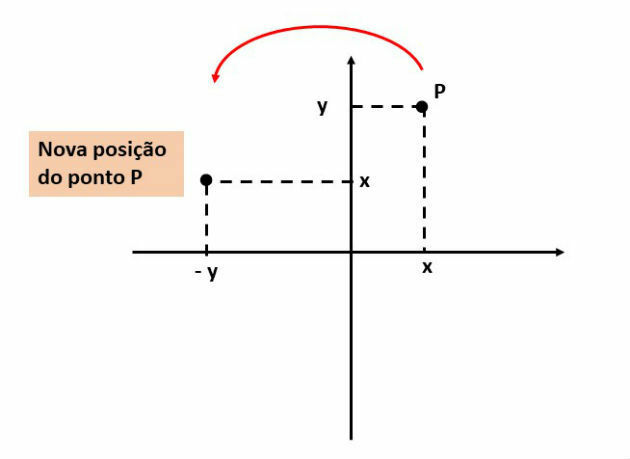
Therefore, point P, which at first was located in the 1st quadrant (positive abscissa and ordinate), moved to the 2nd quadrant (negative abscissa and positive ordinate).

When moving to this new position, the point was rotated counterclockwise, as represented in the image above by the red arrow.

We still need to identify what the rotation angle value was.

By connecting the original position of point P to the center of the Cartesian axis and doing the same in relation to its new position P', we have the following situation:

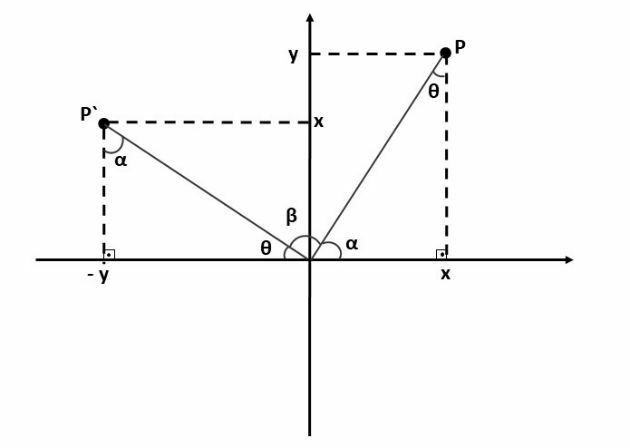
Note that the two triangles indicated in the figure are congruent, that is, they have the same measurements. In this way, their angles are also the same.

In addition, angles α and θ are complementary, as the sum of the internal angles of triangles is equal to 180º and since the triangle is right-angled, the sum of these two angles will be equal to 90º.

Therefore, the angle of rotation of the point, indicated in the figure by β, can only be equal to 90º.

Alternative: b) a 90° rotation of P counterclockwise, with center at (0, 0).

3) Unicamp - 2017

Since a is a real number, consider the matrix A = . So the²⁰¹⁷ it's the same as
The)
B)
ç)
d)

See Answer

First, let's try to find a pattern for the powers, since it's a lot of work to multiply matrix A by itself 2017 times.

Remembering that in matrix multiplication, each element is found by adding the results of multiplying the elements in the row of one by the elements in the column of the other.

Let's start by calculating A²:

The result was the identity matrix, and when we multiply any matrix by the identity matrix, the result will be the matrix itself.

Therefore, the value of A³ will be equal to matrix A itself, because A³ = A². THE.

This result will be repeated, that is, when the exponent is even, the result is the identity matrix and when it is odd, it will be the matrix A itself.

Since 2017 is odd, then the result will be equal to matrix A.

Alternative: b)

4) UFSM - 2011

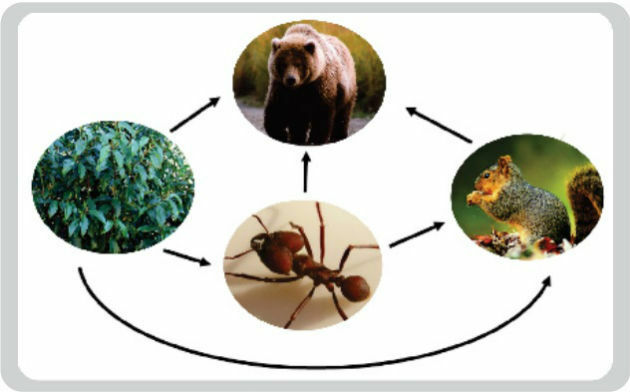
The given diagram represents the simplified food chain of a given ecosystem. Arrows indicate the species the other species feeds on. Attributing a value of 1 when one species feeds on another and zero, when the opposite occurs, we have the following table:

The matrix A = (a_ij)_4x4, associated with the table, has the following training law:

See Answer

Since the row number is indicated by i and the column number indicated by j, and looking at the table, we notice that when i is equal to j, or i is greater than j, the result is zero.

The positions occupied by 1 are those in which the column number is greater than the line number.

Alternative: c)

5) Unesp - 2014

Consider the matrix equation A + BX = X + 2C, whose unknown is the matrix X and all matrices are square of order n. The necessary and sufficient condition for this equation to have a single solution is that:

a) B – I ≠ O, where I is the identity matrix of order n and O is the null matrix of order n.
b) B is invertible.
c) B ≠ O, where O is the null matrix of order n.
d) B – I is invertible, where I is the identity matrix of order n.
e) A and C are invertible.

See Answer

To solve the matrix equation, we need to isolate the X on one side of the equals sign. To do this, let's initially subtract the matrix A on both sides.

A - A + BX = X + 2C - A
BX = X + 2C - A

Now, let's subtract the X, also on both sides. In this case, the equation will be:

BX - X = X - X + 2C - A
BX - X = 2C - A
X.(B - I) =2C - A

Since I is the identity matrix, when we multiply a matrix by the identity, the result is the matrix itself.

So, to isolate the X we must now multiply both sides of the equal sign by the inverse matrix of (B-I), that is:

X. (B - I). (B - I) ^{- 1} = (B - I) ^{- 1}. (2C - A)

Remembering that when a matrix is ​​invertible, the product of the matrix by the inverse is equal to the identity matrix.
X = (B - I) ^{- 1}. (2C - A)

Thus, the equation will have a solution when B - I is invertible.

Alternative: d) B – I is invertible, where I is the identity matrix of order n.

6) Enem - 2012

A student recorded the bimonthly grades of some of his subjects in a table. He noted that the numerical entries in the table formed a 4x4 matrix, and that he could calculate yearly averages for these disciplines using the product of matrices. All tests had the same weight, and the table he got is shown below

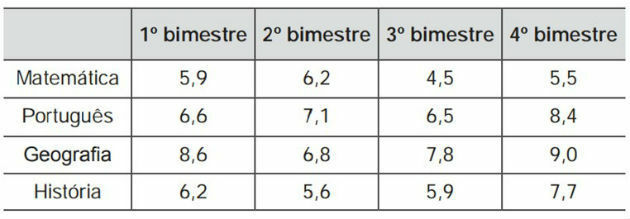
To obtain these averages, he multiplied the matrix obtained from the table by

See Answer

The arithmetic mean is calculated by adding all the values ​​and dividing by the number of values.

Thus, the student must add the grades of the 4 bimesters and divide the result by 4 or multiply each grade by 1/4 and add all the results.

Using matrices, we can achieve the same result by doing matrix multiplication.

However, we must remember that it is only possible to multiply two matrices when the number of columns in one is equal to the number of rows in the other.

As the matrix of notes has 4 columns, the matrix that we are going to multiply must have 4 rows. Thus, we must multiply by the column matrix:

Alternative: and

7) Fuvest - 2012

Consider the matrix , on what The is a real number. Knowing that A admits inverse A^-1 whose first column is , the sum of the elements of the main diagonal of A^-1 it's the same as

a) 5
b) 6
c) 7
d) 8
e) 9

See Answer

Multiplying a matrix by its inverse is equal to the identity matrix, so we can represent the situation by the following operation:

Solving the multiplication of the second row of the first matrix by the first column of the second matrix, we have the following equation:

(to 1). (2a - 1) + (a + 1). (- 1) = 0
2nd² - a - 2a + 1 + (-a) + (-1) = 0
2nd² - 4th = 0
2nd (a - 2) = 0
a - 2 = 0
a = 2

Substituting the value of a in the matrix, we have:

Now that we know the matrix, let's calculate its determinant:

Thus, the sum of the main diagonal will be equal to 5.

Alternative: a) 5

To learn more, see also:

• Matrices
• Determinants
• Sarrus' Rule
• Laplace's Theorem
• Transposed Matrix