Hexagon is a six-sided, six-vertex polygon, so it has six angles. The hexagon is a flat figure, has two dimensions, formed by a closed and simple polygonal line, which does not intersect.
The six sides of the hexagon are straight lines, joined in sequence by the vertices that delimit an inner region.
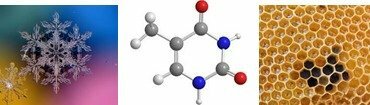
The hexagon appears in many formations in nature, such as beehives, ice crystals or even organic chemistry in structures of carbons and other atoms.
In architecture and engineering, hexagons are used as structural and decorative elements, in screws and keys, to pave roads and other utilities.
The word hexagon comes from the Greek language, where hex refers to the number six and gonia refers to angle. So a figure with six angles.
Elements of Hexagons

A, B, C, D, E and F are the vertices of the hexagon.
the segments are the sides of the hexagon.
are the inner angles.
are the outside angles.
d are the diagonals.
Types of Hexagons
Hexagons are classified into regular and irregular, convex and non-convex, according to the measurements of their sides and angles.
Irregular Hexagons
Irregular hexagons have different sized sides and angles. They are divided into two groups: convex and non-convex.
Convex Irregulars
In convex hexagons, diagonals have all their points in the area of the polygon and no angle is greater than 180°.

Non-Convex Irregulars
In non-convex hexagons, there are diagonals that have points outside the area of the polygon and have angles greater than 180°.

regular hexagons
Regular hexagons have six sides and angles of the same measure, so they are equilateral and equiangle.
All regular hexagons are convex, as no diagonals pass outside the polygon.
A regular hexagon is a composition of six equilateral triangles.
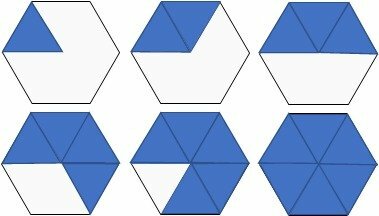
Equilateral triangles are those that have all three sides and angles of the same measurement.
regular hexagon area
The area of the hexagon is calculated using the formula:
Since L is the measure of the hexagon side, the area depends only on L.
Read more at hexagon area.
Perimeter of regular hexagon
The perimeter of the hexagon is the measure of the side multiplied by six.
Hexagon Apothem
The Hexagon Apothema is a line segment that connects the midpoint of one side to the center point of the hexagon.
The apothema of the regular hexagon is calculated by:

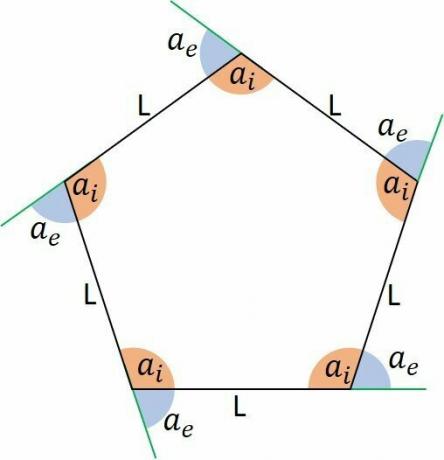
Internal angles of regular hexagons
The measurement of the internal angles of a regular hexagon is 120°.
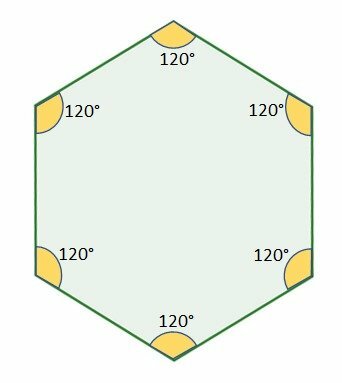
The sum of their internal angles is 720°.
120° x 6 = 720°
External angles of regular hexagons
The measurement of the outside angles of a regular hexagon is 60°.
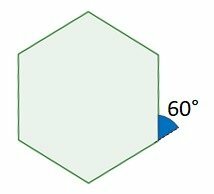
The formula for measuring the outside angles of a regular polygon is:
Where is the measure of the outside angles and n is the number of sides.
If n=6 in the hexagons, we have:
Another way to know the measure of the external angles is through the pair of internal and external angles, as they add up to 180°, being supplementary.
Since the inside angle is 120°, just subtract to determine how many degrees are left to 180°.
180° - 120° = 60°
number of diagonals
The hexagon has 9 diagonals.
There are two ways to determine the number of diagonals:
1st way - counting.
2nd way - through the formula for the diagonals of a polygon.
Where n is the number of sides of the polygon. If n=6 in the hexagon, we have:
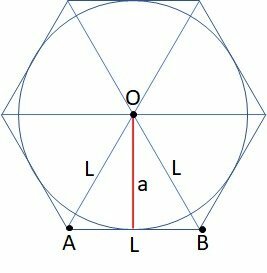
Hexagon inscribed on a circle
A hexagon inscribed on a circle is inside the circle, and its vertices are on the circle.
As the triangle AOB in the figure is equilateral, the measurements of the radius of the circle and the side of the hexagon are equal.
Hexagon circumscribed to a circle
A hexagon is circumscribed to a circle when the circle is inside the hexagon.
The circumference tangents to the sides of the hexagon.
The radius of the circle is equal to the apothema of the hexagon. Replacing, we have:
Then
tiling
Tiling or tessellation is the practice of covering a surface with geometric shapes.
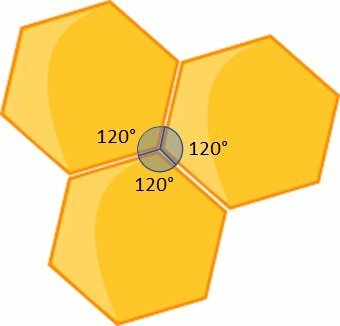
Regular hexagons are among the few polygons that completely fill a surface.
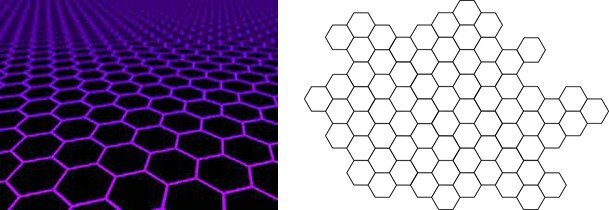
For a regular polygon to be able to tile, that is, fill a surface without leaving gaps, the following geometric condition must be satisfied:
The internal angles of a regular hexagon measure 120°. In hexagon tiling, we notice that three hexagons meet at a vertex. Thus, we have:
120° + 120° + 120° = 360°
Exercise 1
(Enem 2021) A student, resident of the city of Contagem, heard that in this city there are streets that form a regular hexagon. When searching a site for maps, he found that the fact is true, as shown in the figure.
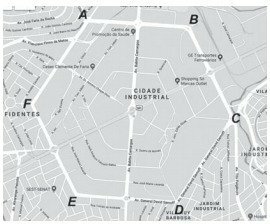
Available at: www.google.com. Accessed on: December 7th. 2017 (adapted).
He noted that the map displayed on the computer screen was at scale 1:20 000. At that moment, he measured the length of one of the segments that form the sides of this hexagon, finding 5 cm.
If this student decides to go completely around the streets that form this hexagon, he will travel, in kilometer,
to 1.
b) 4.
c) 6.
d) 20.
e) 24.
Correct answer: c) 6.
The perimeter of the hexagon is:
P = 6.L
As the side measures 5 cm, we have P = 6.5 = 30 cm
According to the scale, each 1 cm on the map is equivalent to 20 000 cm in the real measurement.
As the course will be 30 cm, we have:
30 x 20,000 = 600,000 cm
to transform it into Km, we divide by 100 000.
600 000 / 100 000 = 6
Therefore, the student will travel 6 km.
Exercise 2
(EEAR 2013) Let be a regular hexagon and an equilateral triangle, both on sides l. The ratio between the apothemas of the hexagon and the triangle is
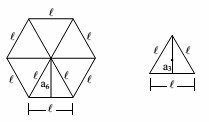
a) 4.
b) 3.
c) 2.
d) 1.
Correct answer: b) 3.
The apothema of the hexagon is:
The apothema of the triangle is:
The ratio between the apothemas of the hexagon and the triangle is:
The ratio is equal to 3.
Exercise 3
(CBM-PR 2010) Consider a traffic sign in the shape of a regular hexagon with sides of 1 centimeter. A regular l-sided hexagon is known to be formed by six l-sided equilateral triangles. As the reading of this sign (plate) depends on the area A of the sign, we have that A, as a function of length l, is given by:
The)
B)
ç)
d)
and)
Correct answer: b)
The area of an equilateral triangle is equal to
In the case of the hexagon the base is equal to the side, so let's replace b with L.
The height of the triangle is equal to the apothem of the hexagon and can be determined by the Pythagorean theorem.
Going back to the triangle formula.
Since the area of the hexagon is equal to six triangles, we multiply the area we calculated by six.
As the measure of the plate is in centimeters, the area will be measured in cm².
In this way, we have:
you may be interested in
- Polygons
- Exercises on Polygons