Exercises on parallel lines cut by a transversal

I do the exercises on parallel lines cut by a transversal line with the list of ten exercises solved step by step, that Toda Matéria prepared for you.

question 1

Since the lines r and s are parallel and t is a line transversal to them, determine the values of a and b.

See Answer

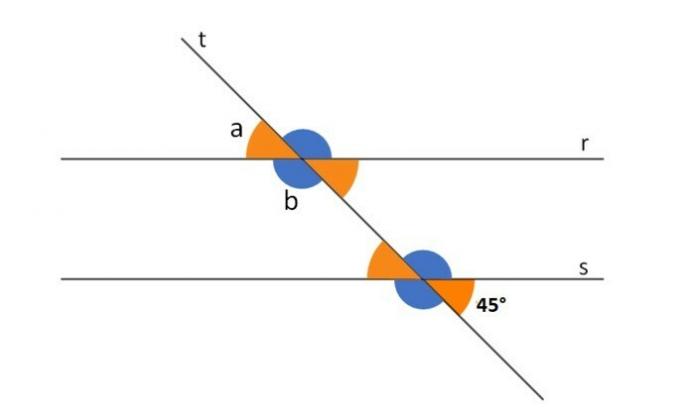
the angles The and 45° are external alternates, so they are equal. Therefore The = 45°.

the angles The and B are supplementary, that is, added together are equal to 180°

The + b = 180°
B = 180° - The
B = 180°- 45°
B = 135°

question 2

Given r and s, two parallel lines and one transversal, determine the values of a and b.

See Answer

The orange angles are corresponding, therefore equal, and we can match their expressions.

6 b plus 140 equals 2 b plus 150 6 b minus 2 b equals 150 minus 140 4 b equals 10 b equals 10 over 4 b equals 2 point 5

At the intersection between r and the transverse, the green and orange angles are supplementary, as they are added together equal to 180°.

Replacing the value of B that we calculate and, solving for The, we have:

a plus 2.2 decimal 5 plus 150 equals 180 plus 5 plus 150 equals 180 plus 155 equals 180 equals 180 minus 155 equals 25 degree sign

question 3

A transverse line t intersects two parallel lines determining eight angles. Sort the angle pairs:

instagram story viewer

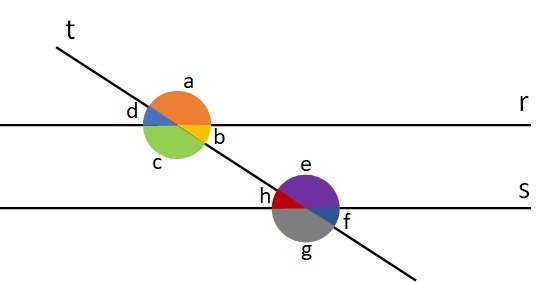
a) Internal alternates.
b) External alternates.
c) Internal collaterals.
d) External collaterals.

See Answer

a) Internal alternates:
ç and and
B and H

b) External alternates:
d and f
The and g

c) Internal collaterals:
ç and H
B and and

d) External collaterals:
d and g
The and f

question 4

Find the value of x where the lines r and s are parallel.

See Answer

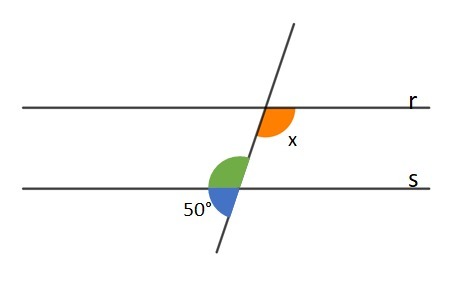
The blue angle of 50° and the adjacent green are supplementary because together they add up to 180°. So we can determine the green angle.

blue + green = 180°
green = 180-50
green=130°

The orange and green angles are alternate internal, so they are equal. Thus, x = 130°.

question 5

Determine the value of the angle x in degrees, the lines r and s being parallel lines.

See Answer

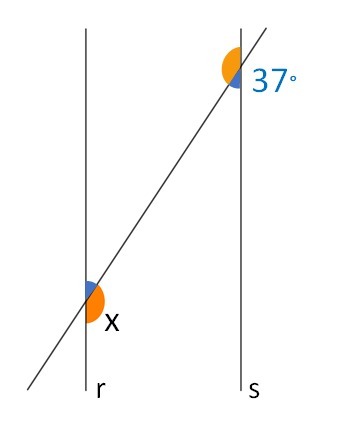
The blue angles are alternate internals, so they are equal. Thus:

37 + x = 180
x=180-37
x=143°

question 6

If r and s are parallel lines, determine the measure of angle a.

See Answer

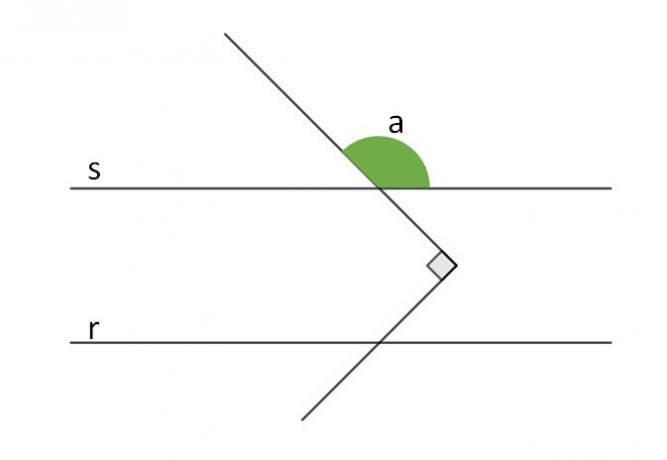
Drawing a line t, parallel to lines r and s, which divides the 90° angle in half, we have two 45° angles, represented in blue.

We can translate the 45° angle and place it on line s, as follows:

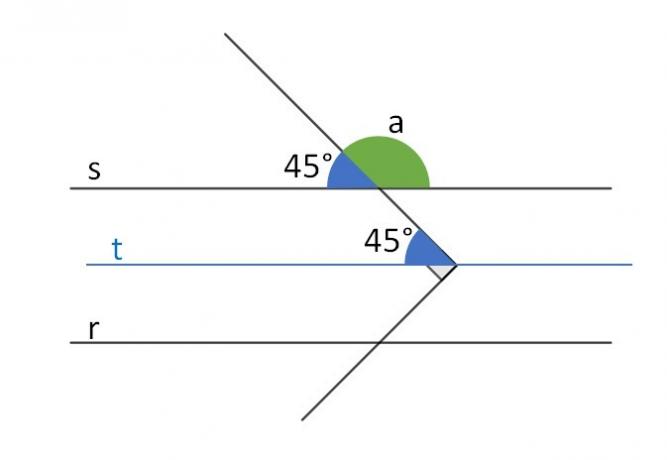
Since the blue angles are corresponding, they are equal. Thus, we have that at + 45° = 180°

at + 45° = 180°
a = 180° - 45°
a = 135°

question 7

If r and s are parallel lines, determine the value of the angle x.

See Answer

To solve this question we will use the Nozzle Theorem, which says:

Each vertex between the parallel lines is a beak;
The sum of the angles of the left-facing nozzles equals the sum of the right-facing nozzles.

25 plus 3 x equal to 43 plus 54 25 plus 3 x equal to 97 3 x equal to 97 minus 25 3 x equal to 72 x equal to 72 over 3 x equal to 24 degree sign

contest questions

question 8

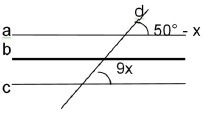
(CPCON 2015) If a, b, c are parallel lines and d is a transverse line, then the value of x is:

a) 9th
b) 10th
c) 45th
d) 7th
e) 5th

See Answer

Correct answer: e) 5°.

9x and 50°-x are corresponding angles, so they are equal.

9x = 50 - x
9x + x = 50
10x = 50
x = 50/10 = 5th

question 9

(CESPE / CEBRASPE 2007)

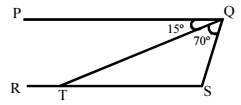
In the figure above, the lines that contain the segments PQ and RS are parallel and the angles PQT and SQT measure 15º and 70º, respectively. In this situation, it is correct to say that the TSQ angle will measure

a) 55th.
b) 85th.
c) 95th.
d) 105th.

See Answer

Correct answer: c) 95th.

The QTS angle measures 15° as it alternates internal to the PQT.

In the triangle QTS, the angles TQS, equal to 70°, the angle QTS, equal to 15° are determined and the angle QST is what we intend to discover.

The sum of the interior angles of a triangle equals 180°. Thus: