Weighted Arithmetic Average, or Weighted Average, is used when some elements are more important than others. These elements are weighted by their weights.
The Weighted Average (MP) considers the values that should influence the final value the most, those with greater weight. For this, each element of the set is multiplied by an assigned value.
Weighted Average Formula
Where: it is the elements of the set that we want to average;
are the weights.
Each element is multiplied by its weight and the result of the multiplications is added together. This result is divided by the sum of the weights.
Weight values are assigned by whoever is averaging, depending on the importance or need for the information.
Example 1
To build a wall, 150 blocks were purchased at store A, which was all the store's stock, for the price of R$ 11.00 per unit. As 250 blocks were needed to build the wall, another 100 blocks were purchased at store B, for R$13.00 per unit. What is the Weighted Average of the block price?
Since we want to average the price, these are the elements and the block quantities are the weights.
Therefore, the weighted average price was BRL 11.80.
Example 2
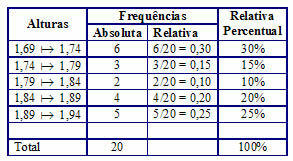
A group of people of different ages were interviewed and their ages noted in the table. Determine the age-weighted arithmetic mean.

As we want the average age, these are the elements and the number of people are the weights.
The Weighted Average of the ages is approximately 36.3 years.
Exercises
Exercise 1
(FAB - 2021) The final classification of a student in a given course is given by the weighted average of the marks obtained in the Mathematics, Portuguese and Specific Knowledge tests.
Suppose a given student's grades are as follows:

Based on this information, calculate the weighted average for that student and check the correct option.
a) 7.
b) 8.
c) 9.
d) 10.
Correct answer: b) 8.
Exercise 2
(Enem - 2017) The performance evaluation of students in a university course is based on the weighted average of the grades obtained in the subjects by the respective number of credits, as shown in the table:
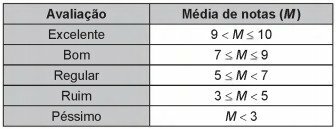
The better the assessment of a student in a given academic term, the greater his priority in choosing subjects for the next term.
A certain student knows that if he obtains a “Good” or “Excellent” assessment, he will be able to enroll in the subjects he desires. He has already taken the tests for 4 of the 5 subjects he is enrolled in, but he has not yet taken the test for subject I, as shown in the table.

In order for him to reach his goal, the minimum grade he must achieve in subject I is
a) 7.00.
b) 7.38.
c) 7.50.
d) 8.25.
e) 9.00.
Correct answer: d) 8.25.
The student needs to achieve at least the good grade and, according to the first table, at least, he should have an average of 7.
We're going to use the weighted average formula where the numbers of credits are the weights, and the grade we're looking for, we'll call it x.
Therefore, the minimum grade he should get in subject I is 8.25.
Exercise 3
A math teacher applies three tests in his course (P1, P2, P3 ), each worth 0-10 points. The student's final grade is the weighted arithmetic average of the three tests, where the weight of the test Pn is equal to n2. To pass the subject, the student must have a final grade greater than or equal to 5.4. According to this criterion, a student will pass this subject, regardless of the grades taken in the first two tests, if he/she gets at least a grade in P3.
a) 7.6.
b) 7.9.
c) 8.2.
d) 8.4.
e) 8.6.
Correct answer: d) 8.4.
The weights of the tests are:
Disregarding the grades of tests 1 and 2, that is, even if you took zero, the average should be 5.4.
Using the weighted average formula, where: N1, N2 and N3 are the grades of tests 1, 2 and 3:
Therefore, the minimum grade must be 8.4.
See too:
- Arithmetic average
- Geometric Mean
- Average, Fashion and Median
- Variance and standard deviation
- Standard deviation
- Statistic
- Statistics - Exercises
- Dispersion Measures