The Braille system is a method of reading for the blind invented by Frenchman Louis Braille. The method consists of an alphabet of embossed dots, which are organized in a table with three lines and two columns forming a rectangle, where at least one stands out in relation to the others. The combinations of these arranged dots are related to symbols that represent simple and accented letters, punctuations, symbols, musical notes, algebraic signs, among others, enabling the visually impaired to read and write any text. For example, the letter A is represented by the following combination:

Due to this type of configuration, the method admits a finite number of characters, as the raised dots are positioned in different places, giving the idea of the following combinations:
Combination of six points grouped one by one - C6.1
Do not stop now... There's more after the advertising ;)
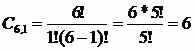
Combination of six points grouped two by two - C6.2

Combination of six points grouped three to three - C6.3
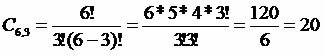
Combination of six points grouped four to four - C6.4

Combination of six points grouped five to five - C6.5

Combination of six points grouped six to six - C6.6

The number of characters that can be represented by the Braille alphabet is the sum of the combinations. C6.1 + C6.2 + C6.3 + C6.4 + C6.5 + C6.6 = 6 + 15 + 20 + 15 + 6 + 1 = 63 possible characters.
by Mark Noah
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Mathematics in the Braille Method"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/a-matematica-no-metodo-braille.htm. Accessed on July 27, 2021.