For what polygons be considered enrolled or circumscribed, there must be a circumference that serves as a basis for this. The fact that they are circumscribed or inscribed concerns a special case of relative positions between the polygon and the circumference.
Before learning to build polygons and circles that are enrolled, it is important to remember the definition of these figures.
Definition of inscribed polygon and inscribed regular polygon
One polygon is said registered in a circumference when all its vertices are points belonging to it.
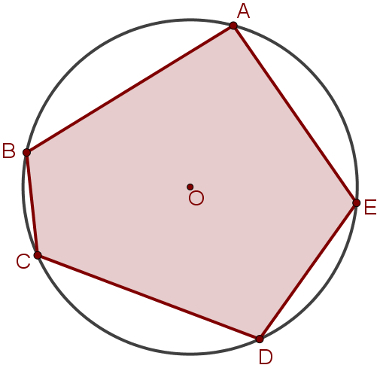
THE construction in polygonsenrolled can be made from points on the circumference. So, to build a pentagon inscribed on a circumference, like the one in the image above, choose five points belonging to it and draw the strings that connect the consecutive points.
The definition of polygonregular enrolled in circumference is the same as any polygon inscribed on it. The difference is that, in this case, the polygon should be regular. This means that all your angles will be the same measurement and all your sides will be congruent.
Techniques for building a regular polygon
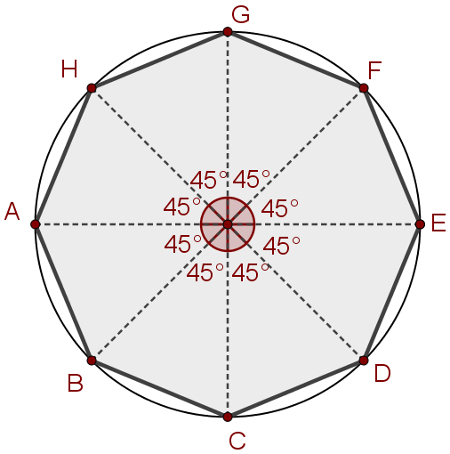
1 - Divide to circumference in x bows with the same length so that x is the number of sides of the polygonregistered in it. The strings connecting the consecutive divisions of arcs will form the inscribed regular polygon.
This division can be done using the rule of three to determine the central angle relative to each arc. In this way, to build the octagon regularregistered, for example, we will divide the circle into eight equal arcs. The center angle relative to them should be 360° divided by 8, which has 45° as a result. After that, just trace the strings that connect the consecutive ends of each bow, as in the image below:
Do not stop now... There's more after the advertising ;)
2 – From the polygonregular, construct the circle that has all its vertices. This construction will always be possible for every regular polygon.
Inscribed circumference
There is also the possibility of a circumference be enrolled at the polygon. For this to happen, it is enough that all sides of this polygon are tangent to the circumference, as shown in the following figure:

Construction of the circle inscribed on the regular polygon
On a polygonregular any, find your center, which will also be the center of circumference. For this, draw two bisector from different sides of the polygon. As it is regular, the meeting point of these lines will be the center of the polygon and, consequently, the center of the circle.
In the following figure, notice the points O and P, which are, respectively, the cent of the circumference and the intersection between a bisector and a side. If the OP segment is used as a radius for the construction of a circle with center O, this circle will be automatically enrolled at the polygon, as shown in the following image:
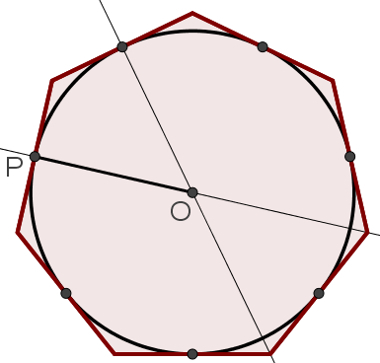
the definition of circumferenceenrolled is equivalent to the definition of polygoncircumscribed. In other words, we could also say that the heptagon in the previous image circumscribes the circle.
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "Construction of inscribed polygons"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/construcao-poligonos-inscritos.htm. Accessed on June 27, 2021.