Study with the 11 questions of 1st and 2nd degree inequalities. Clear your doubts with the solved exercises and prepare yourself with university entrance exams.
question 1
A homeware store offers a set of cutlery for a price that depends on the quantity purchased. These are the options:
Option A: R$94.80 plus R$2.90 per single unit.
Option B: BRL 113.40 plus BRL 2.75 per single unit.
From how many single cutlery purchased, option A is less advantageous than option B.
a) 112
b) 84
c) 124
d) 135
e) 142
Correct answer: c) 124.
Idea 1: write the final price functions in relation to the amount of cutlery purchased.
Option A: PA(n) = 94.8 + 2.90n
Where, PA is the final price of option A and n is the number of single cutlery.
Option B: PB(n) = 113.40 + 2.75n
Where, PB is the final price of option B and n is the number of single cutlery.
Idea 2: write the inequality comparing the two options.
As the condition is that A is less advantageous, let's write the inequality using the sign "greater than", which will represent the number of cutlery after which this option becomes more expensive.
Isolating n from the left side of the inequality and the numerical values from the right side.
Thus, from 124 place settings, option A becomes less advantageous.
question 2
Carlos is negotiating land with a real estate agent. Land A, is on a corner and has the shape of a triangle. The real estate company is also negotiating a strip of land in the shape of a rectangle determined by the following condition: the customer can choose the width, but the length must be five times this measure.

The measure of the width of terrain B so that it has an area greater than that of terrain A is
to 1
b) 2
c) 3
d) 4
e) 5
Correct answer: d) 4
Idea 1: Triangular terrain area.
The area of the triangle is equal to the measure of the base multiplied by the height, divided by two.
Idea 2: rectangular terrain area as a function of width measurement.
Idea 3: inequality comparing the measurements of terrains A and B.
Land area B > Land area A
Conclusion
Terrain A, rectangular, has a larger area than terrain B, triangular, for widths greater than 4 meters.
question 3
A car dealership decided to change its salespeople's payment policy. These received a fixed salary per month, and now the company proposes two forms of payment. Option 1 offers a fixed payment of $1000.00 plus a commission of $185 per car sold. Option 2 offers a salary of $2,045.00 plus a commission of $90 per car sold. After how many cars are sold, option 1 becomes more profitable than option 2?
a) 25
b) 7
c) 9
d) 13
e) 11
Correct answer: e) 11
Idea 1: write wage formulas as a function of the number of cars sold for options 1 and 2.
Option salary 1: 1 000 + 185n
Option salary 2: 2 045 + 90n
Where n is the number of cars sold.
Idea 2: write the inequality comparing the options, using the inequality sign "greater than".
Conclusion
Option 1 becomes more profitable for the seller from 11 cars sold.
question 4
the inequality represents, in hours, the time interval of action of a given drug as a function of time, from the moment a patient ingests it. The drug remains efficient for positive function values.
What is the time interval in which the medicine reacts in the patient's body?
To determine the time interval, we plot the function .
This is a function of the second degree and its curve is a parabola.
Identifying the coefficients
a = -1
b = 3
c = 0
As a is negative, the concavity is turned downwards.
Determining the roots of the equation:
The roots are the points where the function is zero and therefore are the points where the curve cuts the x-axis.

The function takes positive values between 0 and 3.
Therefore, the drug maintains its effect for three hours.
question 5
In a clothing store, a promotion says that if a customer buys one item, he can get a second one, just like the first, for a third of the price. If a customer has BRL 125.00 and wants to take advantage of the promotion, the maximum price of the first piece he can buy, so that he can also take the second, is
a) BRL 103.00
b) BRL 93.75
c) BRL 81.25
d) BRL 95.35
e) BRL 112.00
Correct answer: b) BRL 93.75
Calling the price of the first piece x, the second comes out by x / 3. Since the two together should cost a maximum of R$125.00, we write an inequality using the sign "less than or equal to".
Therefore, the maximum price she can pay for the first piece is R$93.75.
In fact, if x assumes its maximum value of 93.75, the second piece will come out for a third of this value, that is:
93,75 / 3 = 31,25
Thus, the second piece would cost R$31.25.
To check the calculations, let's add up the prices for the first and second part.
93,75 + 31,25 = 125,00
question 6
(ENEM 2020 Digital). In the last election for the presidency of a club, two slates signed up (I and II). There are two types of partners: equity and taxpayers. Votes by equity partners have a weight of 0.6 and by contributing partners have a weight of 0.4. Slate I received 850 votes from equity partners and 4,300 from contributing partners; slate II received 1,300 votes from equity partners and 2,120 from contributing partners. There were no abstentions, blank or null votes, and ticket I was the winner. There will be a new election for the club presidency, with the same number and types of members, and the same slates as the previous election. A consultation made by slate II showed that the equity partners will not change their votes, and that they can count on the votes of the contributing partners from the last election. Thus, in order for it to win, a campaign will be needed with the contributing partners with the objective of changing their votes to slate II.
The smallest number of contributing members who need to change their vote from slate I to slate II for this to be the winner is
a) 449
b) 753
c) 866
d) 941
e) 1 091
Correct answer: b) 753
Idea 1: Plate 1 loses a certain x amount of votes and slate 2 wins that same x amount of votes.
Idea 2: assemble the inequality
As the votes of the equity partners will remain the same, for slate 2 to win the election, it must win x votes from the contributing partners. At the same time, slate 1 must lose those same x votes.
votes plate 2 > votes plate 1
1300. 0.6+ (2120+x). 0,4 > 850. 0.6 + (4300 - x). 0,4
780 + 848 + 0.4x > 510 + 1720 - 0.4x
1628 + 0.4x > 2230 - 0.4x
0.4x + 0.4x > 2230 - 1628
0.8x > 602
x > 602 / 0.8
x > 752.5
Therefore, 753 is the smallest number of contributing partners who need to change their vote from slate I to slate II for this to be the winner.
question 7
(UERJ 2020). A positive integer N that satisfies the inequality é:
a) 2
b) 7
c) 16
d) 17
Correct answer: d) 17
Idea 1: determine the roots
Let's find the roots of this 2nd degree equation using Bhaskara's formula.
Identifying the coefficients
a = 1
b = -17
c = 16
Determining the discriminant, delta.
Determining the roots
Idea 2: sketch the graph
As the coefficient a is positive, the curve of the function has an open concavity upwards and cuts the x axis at points N1 and N2.
It is easy to see that the function takes values greater than zero for N less than 1 and greater than 16.
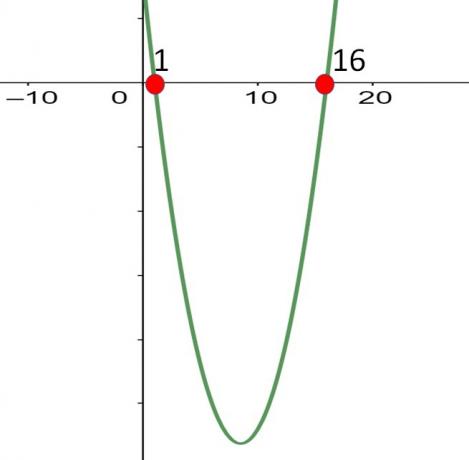
The solution set is: S ={N < 1 and N > 16}.
As the sign of the inequality is greater than ( > ), the values of N = 1 and N = 16 are equal to zero, and we cannot consider them.
Conclusion
The integer among the options that satisfies the inequality is 17.
question 8
(UNESP). Carlos works as a disc jockey (dj) and charges a flat fee of R$100.00, plus R$20.00 per hour, to liven up a party. Daniel, in the same role, charges a flat fee of R$55.00, plus R$35.00 per hour. The maximum length of a party, so that Daniel's hiring doesn't become more expensive than Carlos', is:
a) 6 hours
b) 5 hours
c) 4 hours
d) 3 hours
e) 2 hours
Correct answer: d) 3 hours
Function of Carlos' service price
100 + 20h
Daniel service price function
55 + 35h
If we wanted to know in how many hours the price of their service equals, we would need to equalize the equations.
Daniel Price = Carlos Price
How do we want the price of Daniel's service don't get more expensive than Carlos, we change the equals sign for the less than or equal to .
(inequality of the 1st degree)
Isolating the term with h on one side of the inequality:
For values of h = 3, the service price value equals for both.
Daniel's price for 3 hours of party
55 + 35h = 55 + 35x3 = 55 + 105 = 160
Carlos' price for 3 hours of party
100 + 20h = 100 + 20x3 = 100 + 60 = 160
The statement says: "so that the hiring of Daniel does not become more expensive than that of Carlos". That's why we use the less than or equal to sign.
The maximum duration of a party, so that Daniel's hiring doesn't become more expensive than Carlos', is 3 hours. From 3 am onwards, its hiring becomes more expensive.
question 9
(ENEM 2011). An industry manufactures a single type of product and always sells everything it produces. The total cost to manufacture a quantity q of products is given by a function, symbolized by CT, while the revenue that the company obtains from the sale of the quantity q is also a function, symbolized by FT. The total profit (LT) obtained by selling the quantity q of products is given by the expression LT(q) = FT(q) – CT(q).
Considering the functions FT(q) = 5q and CT(q) = 2q + 12 as revenue and cost, what is the minimum quantity of products that the industry will have to manufacture in order not to have a loss?
a) 0
b) 1
c) 3
d) 4
e) 5
Correct answer: d) 4
Idea 1: not having a loss is the same as having a higher turnover or, at least, equal to zero.
Idea 2: write the inequality and calculate.
According to the statement LT(q) = FT(q) - CT(q). Substituting functions and making greater than or equal to zero.
Therefore, the minimum quantity of products that the industry will have to manufacture in order not to lose is 4.
question 10
(ENEM 2015). Insulin is used in the treatment of patients with diabetes for glycemic control. To facilitate its application, a "pen" was developed in which a refill containing 3mL of insulin can be inserted. To control the applications, the insulin unit was defined as 0.01 mL. Before each application, it is necessary to discard 2 units of insulin, in order to remove possible air bubbles. One patient was prescribed two daily applications: 10 units of insulin in the morning and 10 in the evening. What is the maximum number of applications per refill that the patient can use with the prescribed dosage?
a) 25
b) 15
c) 13
d) 12
e) 8
Correct answer: a) 25
Data
Pen capacity = 3ml
1 unit of insulin = 0.01 mL
Quantity discarded in each application = 2 units
Quantity per application = 10 units
Total amount used per application = 10u + 2u = 12u
Objective: To determine the maximum number of applications possible with the prescribed dosage.
Idea 1: write the inequality "greater than" zero.
Total in mL minus, the total amount per application in units, multiplied by 0.01 mL, multiplied by the number of applications p.
3mL - (12u x 0.01mL)p > 0
3 - (12 x 0.01) p > 0
3 - 0.12p > 0
3 > 0.12p
3 / 0.12 > p
25 > p
Conclusion
The maximum number of applications per refill that the patient can use with the prescribed dosage is 25.
question 11
(UECE 2010). Paul's age, in years, is an even integer that satisfies the inequality . The number representing Paul's age belongs to the set
a) {12, 13, 14}.
b) {15, 16, 17}.
c) {18, 19, 20}.
d) {21, 22, 23}.
Correct answer: b) {15, 16, 17}.
Idea 1: sketch the graph curve of the function f (x) = .
For this, let's determine the roots of the function using Bhaskara's formula.
The coefficients are:
a = 1
b = -32
c = 252
calculating the discriminant
Root calculation
The graph of a 2nd degree function is a parabola, as a is positive the concavity faces up and the curve cuts the x-axis at points 14 and 18.

Idea 2: Identify the values on the chart.
As the inequality of the question is an inequality with a sign "less than", with the value zero on the right side, we are interested in the values of the x axis so that the function is negative.
Conclusion
Therefore, the number representing Paul's age belongs to the set {15, 16, 17}.
learn more about inequalities.
See too
Second degree equation
First degree equation

