THE Cosine Law is used to calculate the measure of one side or an unknown angle of any triangle, knowing its other measures.
Statement and Formulas
The cosine theorem states that:
"In any triangle, the square on one side is the sum of the squares on the other two sides, minus twice the product of those two sides by the cosine of the angle between them.."
Thus, by the law of cosines we have the following relationships between the sides and angles of a triangle:

Examples
1. Two sides of a triangle measure 20 cm and 12 cm and form an angle of 120° between them. Calculate the measurement of the third side.
Solution
To calculate the measure of the third side we will use the law of cosines. For this, let's consider:
b = 20 cm
c = 12 cm
cos α = cos 120º = - 0.5 (value found in trigonometric tables).
Replacing these values in the formula:
The2 = 202 + 122 - 2. 20. 12. (- 0,5)
The2 = 400 + 144 + 240
The2 = 784
a = √784
a = 28 cm
So the third side measures 28 cm.
2. Determine the measure of the side AC and the measure of the angle with vertex at A from the following figure:
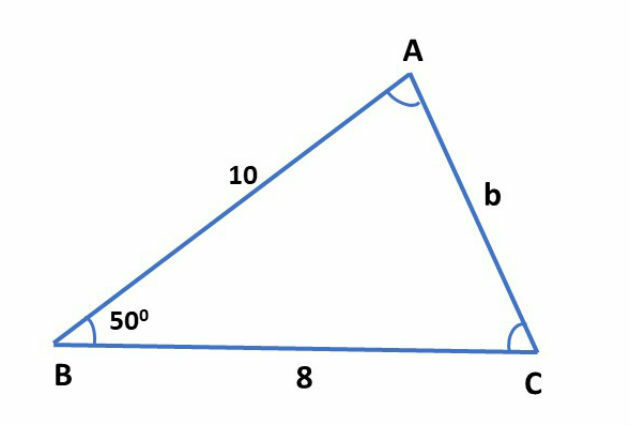
First, let's determine AC = b:
B2 = 82 + 102 – 2. 8. 10. cos 50th
B2 = 164 – 160. cos 50th
B2 = 164 – 160. 0,64279
b ≈ 7.82
Now, let's determine the angle measure by the law of cosines:
82 = 102 + 7,822 – 2. 10. 7,82. cos
64 = 161.1524 – 156.4 cos Â
cos  = 0.62
 = 52º
Note: To find the values of the cosine angles we use the Trigonometric Table. In it, we have the values of angles from 1º to 90º for each trigonometric function (sine, cosine and tangent).
Application
Cosine law can be applied to any triangle. Be it acute-angled (inner angles less than 90°), obtuse-angled (with an inner angle greater than 90°), or rectangle (with an inner angle equal to 90°).

What about Rectangular Triangles?
Let's apply the law of cosines to the side opposite the 90° angle, as indicated below:
The2 = b2 + c2 - 2. B. ç. cos 90º
As cos 90º = 0, the expression above becomes:
The2 = b2 + c2
Which is the same as the expression of Pythagorean theorem. Thus, we can say that this theorem is a particular case of the law of cosines.
Cosine law is suitable for problems where we know two sides and the angle between them and we want to find the third side.
We can still use it when we know the three sides of the triangle and want to know one of its angles.
For situations where we know two angles and only one side and want to determine another side, it is more convenient to use the law of sins.
Definition of Cosine and Sine
The cosine and sine of an angle are defined as trigonometric ratios in a right triangle. The side opposite the right angle (90º) is called the hypotenuse and the other two sides are called the legs, as shown in the figure below:
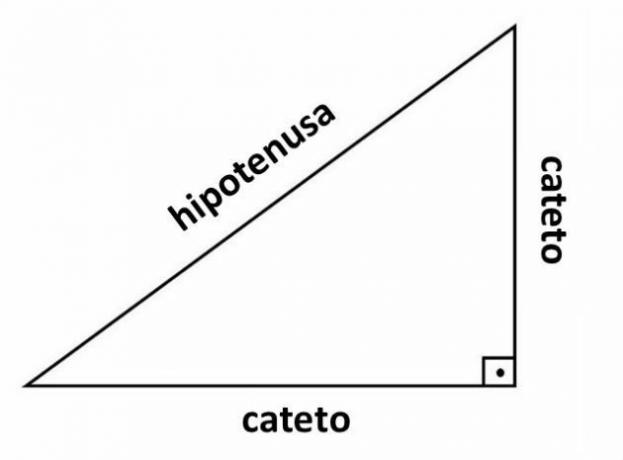
Cosine is then defined as the ratio between the measurement of the adjacent side and the hypotenuse:
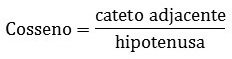
The sine, on the other hand, is the ratio between the measurement of the opposite leg and the hypotenuse.
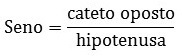
Entrance Exam Exercises
1. (UFSCar) If the sides of a triangle measure x, x + 1 and x +2, then for any x real and greater than 1, the cosine of the largest inner angle of this triangle is equal to:
a) x / x + 1
b) x / x + 2
c) x + 1 / x + 2
d) x – 2/3x
e) x – 3/2x
Alternative e) x – 3 / 2x
2. (UFRS) In the triangle represented in the figure below, AB and AC have the same measure, and the height relative to the side BC is equal to 2/3 of the measure of BC.
Based on these data, the cosine of angle CÂB is:
a) 7/25
b) 7/20
c) 4/5
d) 5/7
e) 5/6
Alternative a) 7/25
3. (UF-Juiz de Fora) Two sides of a triangle measure 8 m and 10 m and form an angle of 60°. The third side of this triangle measures:
a) 2√21 m
b) 2√31 m
c) 2√41 m
d) 2√51 m
e) 2√61 m
Alternative a) 2√21 m
Read more about the topic:
- Trigonometry
- Trigonometry in the Rectangle Triangle
- Trigonometry Exercises in the Right Triangle
- Trigonometric Relations
- Trigonometric Circle
- Trigonometric Functions