Geometric transformations are changes performed on images, such as: transport, mirror, rotate, zoom in or out. They can be made in any figure, whether simple geometric shapes or complex images.
These transformations allow us to create new figures from the original ones or change their position. To carry out these transformations we need to use a reference system and a standard measurement unit, as in the Cartesian plane.
The Cartesian plane is a coordinate system on a plane, where each point has a unique address. It is composed of two numbered axes, the x and the y. Thus, a pair (x, y) gives the exact location of this point.
By conserving shapes, that is, maintaining lengths and angles, we can perform three geometric transformations: translation, rotation and reflection.
For example, when moving an image to a new location, we will be performing a translation. If we rotate it around a point, it's a rotation. If we reflect the figure in relation to an axis, we are doing a reflection.
Translation
Translation consists of moving a figure from one point to another on the plane, maintaining its shape, orientation and size.
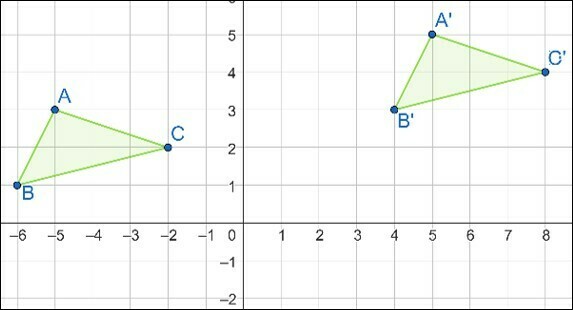
Example
The two triangles in the image below are congruent, that is, equal. We can say that triangle ABC has moved to the second position, represented by triangle A'B'C'.
Reflection
Reflection consists of mirroring an image in relation to a straight line, which can be horizontal, vertical or inclined. This line is called the reflection axis.
In reflection, the coordinates of each point of the original figure are inverted with respect to the reflection axis.
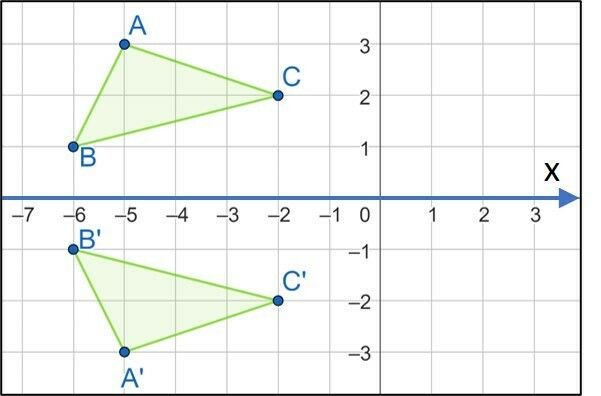
Example
In the reflection in relation to the x axis below, the coordinates of points A, B and C, passed to A', B' and C', like this:
A (-5, 3) ► A' (-5, -3)
B (-6, 1) ► B' (-6, -1)
C (-2, 2) ► C' (-2, -2)
In other words, each point A, B and C is the same distance from the x-axis, of reflection, as the points A', B' and C'.
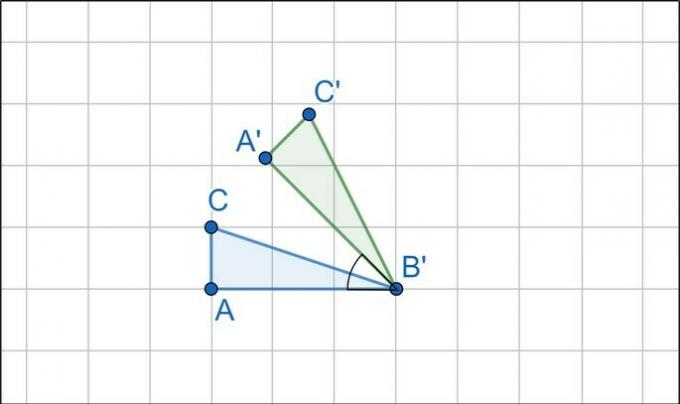
Rotation
Rotating an image consists of rotating it relative to a point in the plane, called the center of rotation. To perform the rotation of a figure, we must consider the orientation of the rotation (clockwise or counterclockwise), and the measure, in degrees, of the angle of rotation.
Example
Triangle ABC has been rotated counterclockwise through a rotation angle of 45°. The center of rotation is point A, which therefore remains fixed.

Geometric reduction and enlargement transformations
When reducing or enlarging, the dimensions of the image are increased or decreased, maintaining the aspect ratio.
In these cases, the angles remain the same, but the lengths and widths increase or decrease. Therefore, the shape of the image is maintained, while its area is changed.
Example

Exercises on geometric transformations
Exercise 1
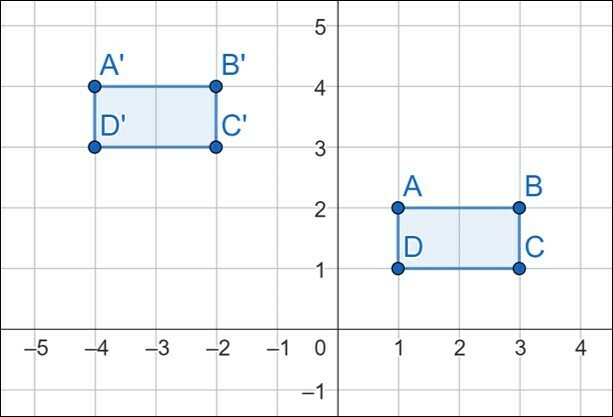
The following quadrilateral ABCD translated which measures in the x and y directions, to the position A'B'C'D'?
Exercise 2
Sketch the reflection of the pentagon from the vertical line.

Exercise 3
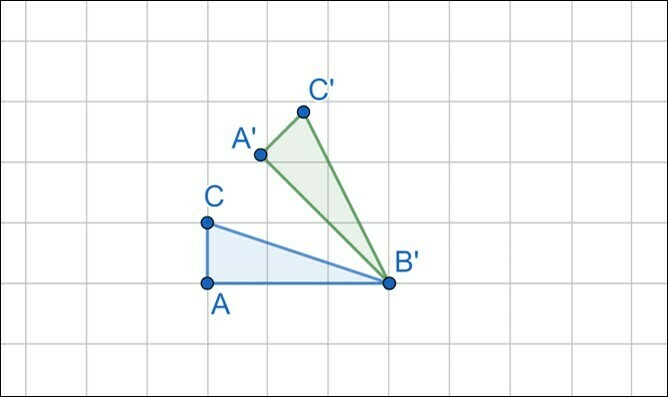
The right triangle below has been rotated with the center of rotation at point B. Answer the direction of rotation and measure the angle of rotation.
See too:
- Geometry
- Plane Geometry
- Geometric Shapes
- polygons
ASTH, Rafael. Geometric transformations: translation, rotation and reflection.All Matter, [n.d.]. Available in: https://www.todamateria.com.br/transformacoes-geometricas/. Access at:
See too
- Time Zones: explanation and calculation
- Circumference
- Solved probability exercises (easy)
- Plane Geometry
- Probability
- Trigonometry in the Right Triangle
- 8th grade math exercises
- Flat Mirrors