The transpose of a matrix A is a matrix that has the same elements as A, but placed in a different position. It is obtained by orderly transporting the elements from the lines of A to the columns of the transpose.
Therefore, given a matrix A = (aij)mxn the transpose of A is At = (a’ji) n x m.
Being,
i: line position
j: column position
Theij: an element of the array at position ij
m: number of rows of the matrix
n: number of columns in the matrix
THEt: transposed matrix of A
Note that the matrix A is of order m x n, while its transpose At is of order n x m.
Example
Find the matrix transposed from matrix B.
As the given matrix is of the 3x2 type (3 lines and 2 columns) its transpose will be of the 2x3 type (2 lines and 3 columns).
To build the transposed matrix, we must write all columns of B as rows of Bt. As indicated in the diagram below:
Thus, the transposed matrix of B will be:
See too: Matrices
Transposed Matrix Properties
- (THEt)t = A: This property indicates that the transpose of a transposed matrix is the original matrix.
- (A + B)t = At + Bt: the transpose of the sum of two matrices is equal to the sum of the transpose of each of them.
- (THE. B)t = Bt. THEt: the transpose of the multiplication of two matrices is equal to the product of the transposes of each of them, in inverse order.
- det (M) = det (Mt): the determinant of the transposed matrix is equal to the determinant of the original matrix.
Symmetric Matrix
A matrix is called symmetric when, for any element of matrix A, the equality aij = theji it's true.
Matrices of this type are square matrices, that is, the number of rows is equal to the number of columns.
Every symmetric matrix satisfies the following relationship:
A = At
Opposite Matrix
It is important not to confuse the opposite matrix with the transposed one. The opposite matrix is one that contains the same elements in the rows and columns, however, with different signs. Thus, the opposite of B is –B.
Inverse matrix
THE inverse matrix (indicated by the number –1) is the one where the product of two matrices is equal to a square identity matrix (I) of the same order.
Example:
THE. B = B. A = Ino (when matrix B is inverse of matrix A)
Entrance Exam Exercises with Feedback
1. (Fei-SP) Given the Matrix A = 
, being thet its transpose, the determinant of matrix A. THEt é:
to 1
b) 7
c) 14
d) 49
Alternative d: 49
2. (FGV-SP) A and B are matrices and At is the transposed matrix of A. if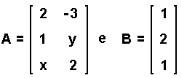 
, then the matrix At. B will be null for:
a) x + y = –3
b) x. y = 2
c) x/y = –4
d) x. y2 = –1
e) x/y = –8
Alternative d: x. y2 = –1
3. (UFSM-RS) Knowing that the matrix
is equal to transposed, the value of 2x + y is:
a) –23
b) -11
c) -1
d) 11
e) 23
Alternative c: -1
Read too:
- Matrices - Exercises
- Types of Matrices
- Matrices and Determinants
- Matrix Multiplication
