O volume of a geometric solid is a magnitude that represents the space that this geometric solid occupies. The most common volume measurements are cubic units, such as cubic meters m³, their multiples and their sub-multiples. The main geometric solids are prisms, pyramids, cone, cylinder and sphere, and each of them has specific formulas for calculating volume.
Read too: What are the differences between flat and spatial figures?
Summary on the volume of geometric solids
Each geometric solid has a different formula for calculating its volume.
The volume of a solid is measured in cubic units, such as cubic meters, cubic centimeters, and so on.
Formula to calculate the prism volume:
V = AB · H
Formula to calculate the volume of the pyramid:
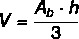
Formula for calculating the volume of a cylinder:
V = πr² · h
Formula for calculating the volume of a cone:
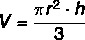
Formula to calculate the volume of the sphere:
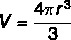
Do not stop now... There's more after the advertising ;)
volume measurements
We call volume the space that a given
geometric solid occupy, soon, it only makes sense to calculate the volume of three-dimensional objects. To measure the volume, we use as a unit of measure the cubic meter (m³) and its multiples, that are:cubic decameter (dam³)
cubic hectometer (hm³)
cubic kilometer (km³)
There are also the submultiples of the cubic meter, that are:
cubic decimeter (dm³)
cubic centimeter (cm³)
cubic millimeter (mm³)
See too: What are the length measurements?
How to calculate the volume of geometric solids?
Finding the volume of a geometric solid is fundamental for many daily activities, for example, to know the capacity of a shed, to know the space occupied by a certain piece of furniture in our House.We calculate the volume using specific formulas for each of the geometric solids. Now let's look at the volume formulas for the main geometric solids in spatial geometry.
prism volume
starting with prism, one of the most common solids in everyday life. The prism is all geometric solid that it has two equal bases and side faces formed by parallelepipeds, for example, shoeboxes, buildings, among other objects.
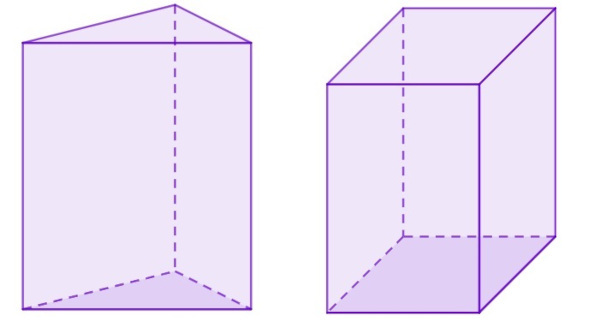
To calculate the prism volume, it is necessary to know the base area, which can be formed by any polygon. O prism volume is calculated by the product of the base area and the prism height.
Vprisms = AB · H
THEB → base area
h → prism height
There are two particular cases of very recurrent prisms, namely the cube and the rectangular parallelepiped.
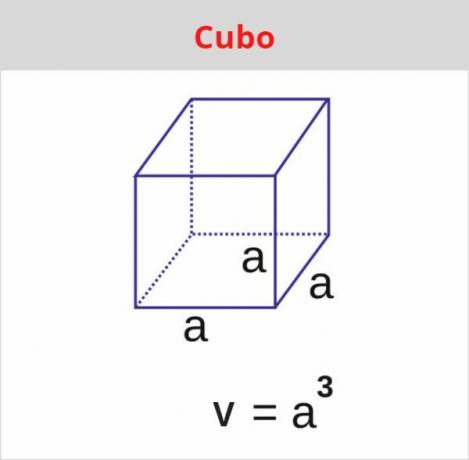
→ cube volume
Starting with the cube, we know that it has all edges congruent. So, to calculate the volume of the cube, we know that the area of the square is equal to the square of the edge. To calculate the volume, we multiply by the height, which, in the case of the cube, is also equal to the edge measurement. Thus, the cube volume is given by:
→ Rectangle parallelepiped volume
the volume of paving stone rectangle can be found when we multiply its three dimensions:

Example 1:
Calculate the volume of a cube-shaped prism whose edges measure 5 cm each:
V = a³
V = 5³
V = 125 cm³
Example 2:
Calculate the prism volume below:

as your base is a rectangle, the base area is the product between 12 and 5. To find the volume, we'll multiply the base area by the height, so we have to:
V = AB · H
V = 12 · 5 · 15
V = 60 · 15
V = 900 cm³
→ Video lesson on prism volume
volume of the pyramid
THE pyramid is the geometric solid that has the base formed by a polygon and the side faces formed by a triangle, connecting the base vertices to a point outside the base known as the pyramid vertex. Like the prism, the pyramid can also have different bases.
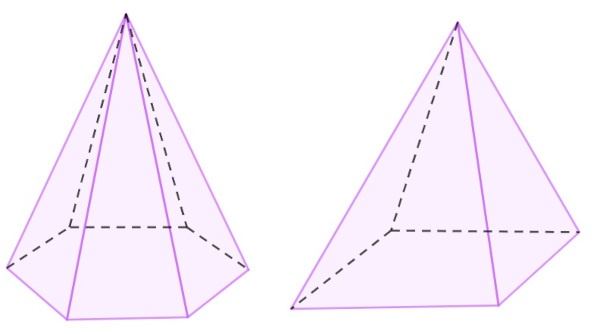
To calculate the pyramid volume, it is necessary to calculate the area of the base. The volume of the pyramid is given by the formula:
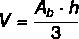
Example:
Calculate the volume of a pyramid that has a square base with sides measuring 6 meters and a height of 10 meters.
As the base of the pyramid is a square, its area will be the squared side, so we have to:

Read too: Pyramid trunk - figure obtained from a cross section in a pyramid
cylinder volume
O cylinder is the geometric solid that has two circular bases of the same radius. rated one round body due to its rounded shape, this geometric solid is quite recurrent in packaging such as chocolate and other products.
To calculate the volume of a cylinder, we only need the measurement of its radius and its height:
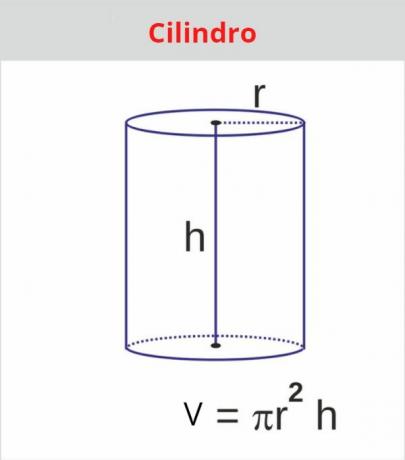
Example:
Calculate the volume of the following cylinder (use π = 3.1):

V = πr² h
V = 3.1 · 3² · 8
V = 3.1 · 9 · 8
V = 3.1 · 72
V = 223.2 cm³
→ Video lesson on cylinder volume
cone volume
O cone it is also classified as a round body. He has a base formed by a circle and a vertex. To calculate the cone volume, it is also necessary to know its height and the radius of its base:
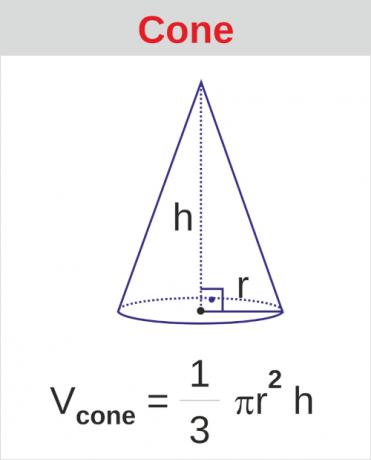
Example:
Calculate the volume of the cone:

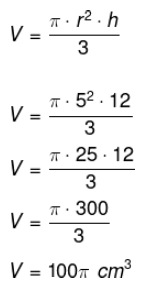
sphere volume
THE ball it is also a common format in everyday life, like the balls we use to play certain sports, in addition to being a common format in nature. To calculate the volume of the sphere, it is only necessary to know its radius.:
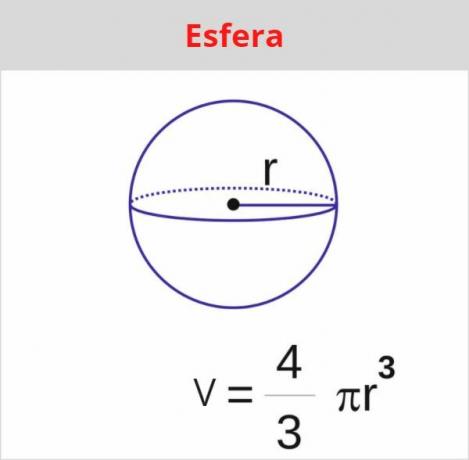
Example:
Calculate the volume of the sphere that has a radius equal to 2 meters (use π = 3.1):

See too: What are the elements of a sphere?
Solved exercises on volume of geometric solids
Question 1 - (Fei) From a wooden beam with a square section of side L = 10 cm, extract a wedge of height h = 15 cm, as shown in the figure. The volume of the wedge is:
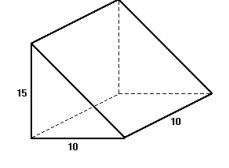
A) 250 cm³
B) 500 cm³
C) 750 cm³
D) 1000 cm³
E) 1250 cm³
Resolution
Alternative C
Since the base is a triangle, we know that:

Now we will calculate the prism volume:
V = AB · H
V = 75 · 10
V = 750 cm³
Question 2 - (FGV) The volume of a sphere of radius r is given by V = 4/3 π r³. A spherical shaped reservoir has a volume of 36 π cubic meters. Let A and B be two points on the spherical surface of the reservoir and let m be the distance between them. The maximum value of m in meters is:
A) 5.5
B) 5
C) 6
D) 4.5
E) 4
Resolution
Alternative C
The greatest distance between two points on a sphere is the diameter of that sphere. Since we know the volume of the sphere, then it is possible to calculate its radius:
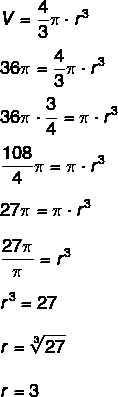
Since the greatest possible distance is equal to the diameter, that is, it measures twice the radius, so d = 6.
By Raul Rodrigues de Oliveira
Maths teacher

