tithesperiodic they are infinite and periodic numbers. Infinite, for they have no end, and periodicals, because certain parts of them are repeated, that is, they have a period. Furthermore, periodic decimals can be represented in fractional form, that is, we can say that they are rational numbers.
if divide the numerator of a fraction by the denominator and we find a tenth, then that fraction will be called generating fraction. Tithes can be classified as simple and compound.
Read too: Fun Facts About Dividing Natural Numbers
Types of periodic tithes
simple periodic tithe
É characterized by not having antiperiod, that is, the period (repeating part) comes right after the comma. See some examples:
Examples
The) 0,32323232…
Time course → 32
B) 0,111111…
Time course → 1
ç) 0,543543543…
Time course → 543
d) 6,987698769876…
Time course → 9876
Observation: We can represent a periodic decimal with a slash over the period, for example the number 6.98769876... it can be written as follows:

compound periodic tithe
It's the one that has antiperiod, that is, between the comma and the period there is a number that does not repeat.
Examples
The) 2,3244444444…
Time course → 4
Antiperiod → 32
B) 9,123656565…
Time course → 65
Antiperiod → 123
ç) 0, 876547654…
Time course → 7654
Antiperiod → 8

generating fraction
Periodic tithes can be represented in the form of fraction, what makes them rational numbers. When a fraction generates a periodic decimal, it is called generating fraction. The process to find the generating fraction it's simple, follow the step by step:
Example 1
The tithe used in the example will be: 0.323232…
Step 1 – Name the tithe an unknown.
x = 0.323232...
Step 2 – Use the principle of equivalence, that is, if we operate on one side of equality, we must perform the same operation on the other side to maintain equivalence. So, let's multiply the tithe by one power of 10 until the period is before the comma.
Note that the period in this case is 32, so we must do the multiplication by 100. Also notice that the number of digits in the period gives us the number of zeros that the power of 10 must have. Thus:
100 · x = 0.323232... · 100
100x = 32.32332232...
Step 3 – Subtract the equation from step 2 from the equation from step 1.

Subtracting term by term, we have:
100x - x = 32.323232... - 0.323232...
99x = 32
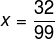
Now see the example where the method for compound tithes is applied.
Read too: Properties of multiplication that facilitate mental calculation
Example 2
The composite tithe used will be: 9,123656565….
Before performing the first step, note that:
9,123656565… = 9 + 0, 123656565…
Let's work only with the tithe, and at the end, just add 9 to the generating fraction.
Step 1 – Name the tithe an unknown.
x = 0.123656565…
Step 2 – Multiply it by a power of 10 until the non-periodic part is before the comma. In this case, the multiplication must be by 100, as the non-periodic part has three digits.
100 · x = 0.123656565… ·100
100x = 123.656565…
Step 3 – Multiply it again by a power of 10 until the periodic part is before the comma. Since the periodic part (65) has two digits, we multiply both sides by 100, like this:
100 ·100x = 123.656565… ·100
10000x = 12365.656565…
Step 4 – Finally, subtract the equation obtained in step 3 from the equation obtained in step 2.
10000x – 100x = 12365.656565… – 123.656565…
9,900 x = 12,242
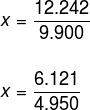
Remember that you still need to add 9 to this fraction, so:

by Robson Luiz
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-dizima-periodica-e-fracao-geratriz.htm
