Function: what is it, types of functions and graphics

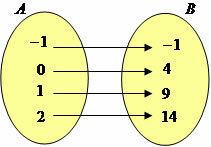
In Mathematics, function corresponds to an association of the elements of two sets, that is, the function indicates how the elements are related.

For example, a function from A to B means to associate each element belonging to the set A with a only element that makes up the set B, so a value of A cannot be linked to two values of B.

Function notation: f: A → B (read: f from A to B).

Representation of functions

in a role f: A → B set A is called domain (D) and set B is called counterdomain (CD).

An element of B related to an element of A is named image by the function. Grouping all the images of B we have an image set, which is a subset of the domain.

Example: Note the sets A = {1, 2, 3, 4} and B = {1, 2, 3, 4, 5, 6, 7, 8}, with the function that determines the relationship between the elements f: A → B is x → 2x. Therefore, f(x) = 2x and each x in set A is transformed into 2x in set B.

Note that the set of A {1, 2, 3, 4} are the inputs, "multiply by 2" is the function and the values ​​of B {2, 4, 6, 8}, which bind to the elements of A, are the output values.

So for this role:

• The domain is {1, 2, 3, 4}
• The counterdomain is {1, 2, 3, 4, 5, 6, 7, 8}
• The image set is {2, 4, 6, 8}

Types of Functions

Roles are classified according to their properties. Check out the main types below.

Overjet function

At surjective function the counterdomain is the same as the image set. Therefore, every element of B is the image of at least one element of A.

Notation: f: A → B, occurs to Im (f) = B

Example:

For the above function:

• The domain is {-4, -2, 2, 3}
• The counterdomain is {12, 4, 6}
• The image set is {12, 4, 6}

Injector function

At injection function all elements of A have distinct counterparts in B and none of the elements of A share the same image in B. However, there may be elements in B that are not related to any element in A.

Example:

For the above function:

• The domain is {0, 3, 5}
• The counterdomain is {1, 2, 5, 8}
• The image set is {1, 5, 8}

Bijector function

At bijtora function sets have the same number of related elements. This function receives this name because it is both injecting and surjective.

Example:

For the above function:

• The domain is {-1, 1, 2, 4}
• The counterdomain is {2, 3, 5, 7}
• The image set is {2, 3, 5, 7}

inverse function

THE inverse function it is a type of bijector function, so it is both surjective and injecting at the same time.

Through this type of function it is possible to create new functions by inverting the elements.

composite function

THE composite function is a type of mathematical function that combines two or more variables.

Two functions, f and g, can be represented as a function composed of:

fog (x) = f (g(x))
gof(x) = g(f(x))

modular function

THE modular function associates elements into modules and their numbers are always positive.

related function

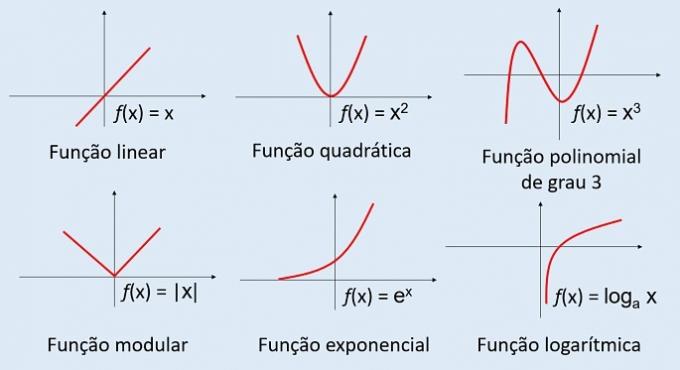
THE affine function, also called the 1st degree function, has a growth rate and a constant term.

f (x) = ax + b

a: slope
b: linear coefficient

linear function

THE linear function is a particular case of the affine function, being defined as f(x) = ax.

When the value of the coefficient (a) that accompanies the x of the function is equal to 1, the linear function is an identity function.

quadratic function

THE quadratic function it is also called the 2nd degree function.

f(x) = ax²+ bx + c, where a ≠ 0

a, b and c: coefficients of the polynomial function of degree 2.

logarithmic function

THE logarithmic function of base a is represented by f(x) = log_The x, being a positive real and a ≠ 1.

When we invert the logarithmic function, we have an exponential function.

exponential function

THE exponential function presents a variable in the exponent and the base is always greater than zero and different from one.

f(x) = a^x, where a > 0 and a ≠ 0

polynomial function

THE polynomial function is defined by polynomial expressions.

f(x) = a_no. x^no + the_{n - 1}. x^{n - 1} + ...+a₂ . x² + the₁. x + a₀

The_no, a_n-1,..., a₂, a₁, a₀: complex numbers
n: integer
x: complex variable

Trigonometric Functions

At trigonometric functions are related to turns in the trigonometric cycle, such as:

Sine Function: f (x) = sin x
Cosine Function: f (x) = cos x
Tangent Function: f (x) = tg x

Graph of a function

The way an element y relates to an element x is expressed through a graph, which gives us an idea of ​​the behavior of the function.

Each point on the graph is given by an ordered pair of x and y, where x is the input value and y is the result of the relationship defined by the function, that is, x → function → y.

To build a graph, each x element of the function must be placed on the horizontal axis (abscissa) and the y elements are placed on the vertical axis (ordinate).

Check out some examples of function graphs.

Use the following exercise lists to test your knowledge of functions.

• Exercises on affine function (1st degree)
• Exercises on quadratic function (2nd degree)
• Exercises on exponential function