Trigonometry is an important theme in Mathematics that makes it possible to know sides and angles in a right triangle, through the sine, cosine and tangent, in addition to other trigonometric functions.
To improve your studies and expand your knowledge, follow the list of 8 exercises, plus 4 entrance exam questions, all solved step by step.
Exercise 1
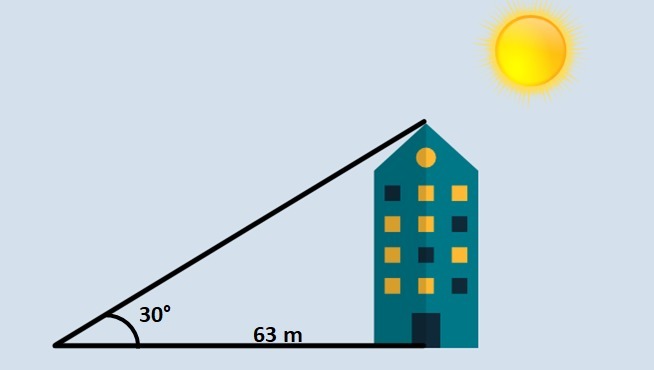
Observing in the morning the shadow of a building on the ground, one person found that it measured 63 meters when the sun's rays made an angle of 30° with the surface. Based on this information, calculate the height of the building.
Correct answer: Approximately 36.37 m.
The building, the shadow and the sun's ray determine a right triangle. Using the 30° angle and the tangent, we can determine the height of the building.
Since the height of the building is h, we have:
Exercise 2
On a circumference with a diameter of 3, a segment AC, called a chord, forms a 90° angle with another chord CB of the same length. What is the measure of the strings?

Correct answer: The length of the rope is 2.12 cm.
As the segments AC and CB form an angle of 90° and are of the same length, the triangle formed is isosceles and the base angles are equal.
Since the sum of the internal angles of a triangle is equal to 180° and we already have an angle of 90°, there are another 90° left to be divided equally between the two base angles. Thus, the value of these is equal to 45º each.
Since the diameter is equal to 3 cm, the radius is 1.5 cm and we can use the cosine of 45° to determine the length of the string.
Exercise 3
A cyclist participating in a championship approaches the finish line at the top of a slope. The total length of this last part of the test is 60 m and the angle formed between the ramp and the horizontal is 30°. Knowing this, calculate the vertical height the cyclist needs to climb.

Correct answer: The height will be 30 m.
Calling the height of h, we have:
Exercise 4
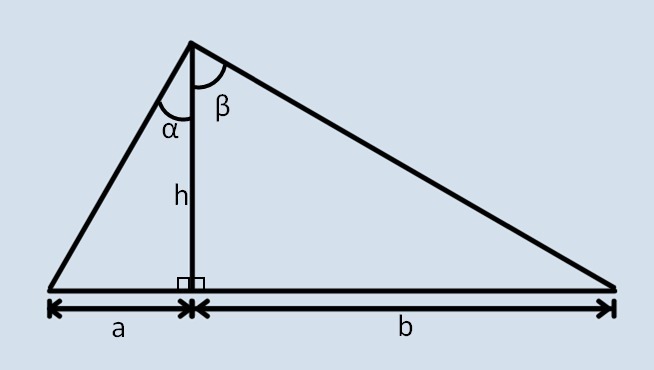
The following figure is formed by three triangles where the height h determines two right angles. The element values are:
α = 30°
β = 60°
h = 21
Find the value of a+b.
Right answer:
We can determine the measurements of segments a and b using the tangents of the given angles.
Calculation of a:
Calculation of b:
Thus,
Exercise 5
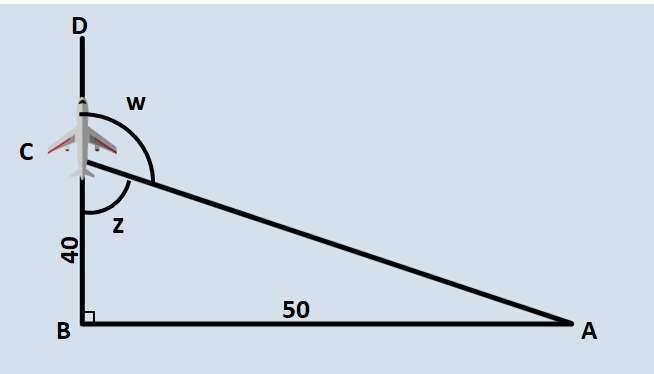
A plane took off from city A and flew 50 km in a straight line until it landed in city B. Afterwards, it flew another 40 km, this time heading towards city D. These two routes are at a 90° angle to each other. However, due to unfavorable weather conditions, the pilot received a communication from the control tower informing him that he could not land in city D and that he should return to city A.
In order to make the U-turn from point C, the pilot would have to make a turn of how many degrees to the right?
Consider:
sin 51° = 0.77
cos 51° = 0.63
tan 51° = 1.25
Correct answer: The pilot must make a turn of 129° to the right.
Analyzing the figure, we see that the path forms a right triangle.
Let's call the angle we're looking for W. Angles W and Z are supplementary, that is, they form a shallow angle of 180°.
Thus, W + Z = 180°.
W = 180 - Z (equation 1)
Our task now is to determine the Z angle and, for that, we are going to use its tangent.
We must ask ourselves: What is the angle whose tangent is 1.25?
The problem gives us this data, tan 51° = 1.25.
This value can also be found in a trigonometric table or with a scientific calculator, using the function:
Substituting the value of Z in equation 1, we have:
W = 180° - 51° = 129°
Exercise 6
A ray of monochromatic light when passing from one medium to another, suffers a deviation towards it. This change in its propagation is related to the refraction indices of the media, as shown in the following relationship:
Snell's Law - Descartes
Where i and r are the angles of incidence and refraction and, n1 and n2, the refractive indices of means 1 and 2.
When hitting the surface of separation between air and glass, a ray of light changes its direction, as shown in the figure. What is the refractive index of glass?
Data: Air refraction index equal to 1.

Correct answer: The refractive index of the glass is equal to .
Replacing the values we have:
Exercise 7
To drag a wooden log into his workshop, a locksmith tied a rope to the log and pulled it ten feet across a horizontal surface. A force of 40 N through the string made an angle of 45° with the direction of travel. Calculate the work of the applied force.
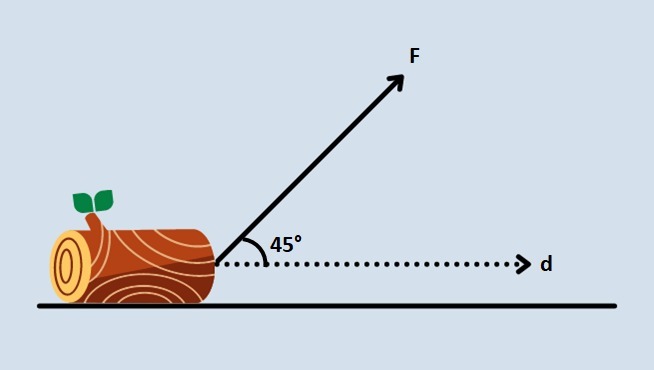
Correct answer: The work performed is approximately 84.85 J.
Work is a scalar quantity obtained by the product of force and displacement. If the force does not have the same direction as the displacement, we must decompose this force and consider only the component in this direction.
In this case, we must multiply the magnitude of the force by the cosine of the angle.
So we have:
Exercise 8
Between two mountains, the residents of two villages had to travel a hard way up and down. To resolve the situation, it was decided that a cable-stayed bridge would be built between villages A and B.
It would be necessary to calculate the distance between the two villages by the straight line on which the bridge would be stretched. As residents already knew the height of the cities and the angles of climb, this distance could be calculated.
Based on the diagram below and knowing that the height of the cities was 100 m, calculate the length of the bridge.
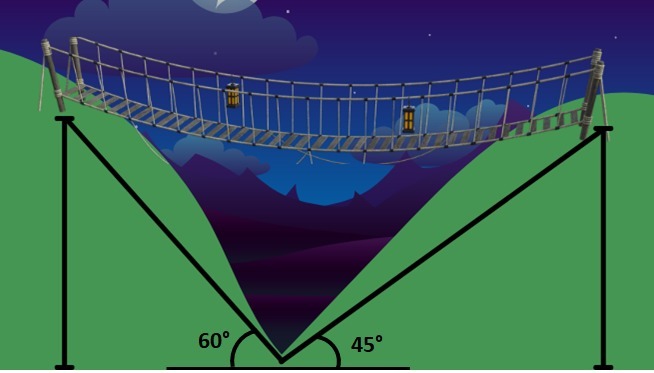
Correct answer: The bridge should have a length of approximately 157.73 m.
The bridge length is the sum of the sides adjacent to the given angles. Calling the height of h, we have:
Calculation with the 45° angle
Calculation with an angle of 60°
To determine the bridge length, we sum the obtained values.
question 1
Cefet - SP
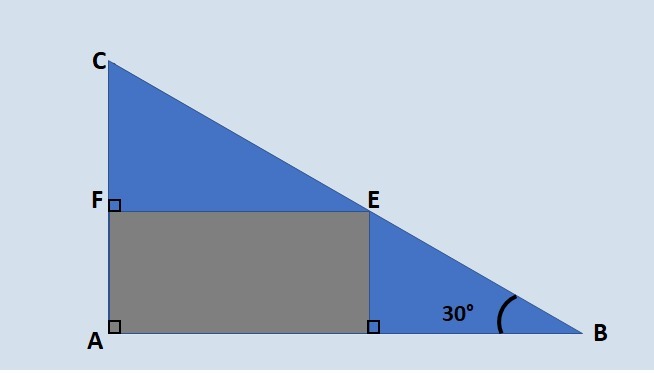
In the triangle ABC below, CF = 20 cm and BC = 60 cm. Mark the measurements of the AF and BE segments respectively.
a) 5, 15
b) 10, 20
c) 15, 25
d) 20, 10
e) 10, 5
Answer: b) 10, 20
To determine AF
We note that AC = AF + CF, so we have to:
AF = AC - CF (equation 1)
CF is given by the problem, being equal to 20 cm.
AC can be determined using 30° sine.
BC is provided by the problem, being equal to 60 cm.
Substituting in equation 1, we have:
To determine BE
First observation:
We verify that the figure inside the triangle is a rectangle, due to the right angles determined in the figure.
Therefore, their sides are parallel.
Second observation:
The BE segment forms a right-angled triangle with an angle of 30° where: the height is equal to AF, which we have just determined, and BE is the hypotenuse.
Making the calculation:
We use 30° sine to determine BE
question 2
EPCAR-MG
An airplane takes off from point B under a constant inclination of 15° to the horizontal. 2 km from B is the vertical projection C of the highest point D of a 600 m high mountain range, as shown in the figure.
Data: cos 15° = 0.97; sin 15° = 0.26; tg 15° = 0.27

It is correct to say that:
a) The plane will not collide with the saw before reaching 540 m in height.
b) There will be a collision between the plane and the saw at a height of 540 m.
c) The plane will collide with the saw in D.
d) If the plane takes off 220 m before B, keeping the same inclination, there will be no collision of the plane with the saw.
Answer: b) There will be a collision between the plane and the saw at a height of 540 m.
First, it is necessary to use the same multiple of the length measurement unit. Therefore, we will go 2 km to 2000 m.
Following the same initial flight conditions, we can predict the height at which the plane will be in the vertical projection of point C.
Using the 15° tangent and defining the height as h, we have:
question 3
ENEM 2018
To decorate a straight circular cylinder, a rectangular strip of transparent paper will be used, on which a diagonal that forms 30° with the lower edge is drawn in bold. The radius of the base of the cylinder measures 6/π cm, and when winding the strip, a line in the shape of a helix is obtained, as shown in the figure.
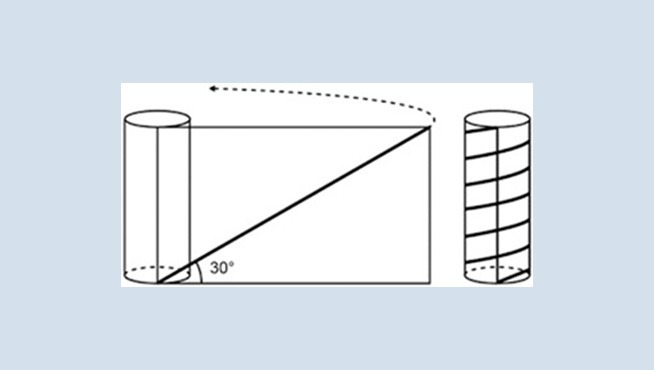
The measurement value of the height of the cylinder, in centimeters, is:
a) 36√3
b) 24√3
c) 4√3
d) 36
e) 72
Answer: b) 24√3
Observing the figure we notice that 6 turns were made around the cylinder. As it is a straight cylinder, anywhere in its height we will have a circle as the base.
To calculate the measure of the base of the triangle.
The length of a circle can be obtained from the formula:
Where r is the radius e, equal to ,we have:
How are 6 laps:
We can use the 30° tan to calculate height.
question 4
ENEM 2017
Rays of sunlight are reaching the surface of a lake at an X angle with its surface, as shown in the figure.
Under certain conditions, it can be assumed that the luminous intensity of these rays, on the lake surface, is given approximately by I(x) = k. sin (x), k being a constant, and assuming that X is between 0° and 90°.
When x = 30º, the luminous intensity is reduced to what percentage of its maximum value?
A) 33%
B) 50%
C) 57%
D) 70%
E) 86%
Answer: B) 50%
Replacing the 30° sine value in the function, we obtain:
Having reduced the value of k by half, the intensity is 50%.
Practice more exercises in:
Trigonometry Exercises
Expand your knowledge with:
Trigonometry in the right triangle
Metric Relations in the Rectangle Triangle
Trigonometry