The cone volume is calculated by product between the base area and the height measurement, and the result divided by three.
Remember that volume means the capacity of a spatial geometric figure.
Check out in this article some examples, solved exercises and entrance exams.
Formula: How to Calculate?
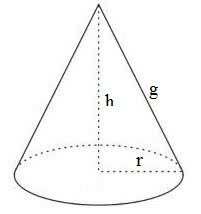
The formula to calculate the cone volume is:
V = 1/3 π.r2. H
Where:
V: volume
π: constant equivalent to approximately 3.14
r: lightning
h: height
Attention!
The volume of a geometric figure is always calculated in m3, cm3, etc.
Example: Solved Exercise
Calculate the volume of a straight circular cone whose base radius is 3 m and generator 5 m.
Resolution
First, we must calculate the height of the cone. In this case, we can use the Pythagorean theorem:
H2 + r2 = g2
H2 + 9 = 25
H2 = 25 – 9
H2 = 16
h = 4 m
After finding the height measurement, just insert in the volume formula:
V = 1/3 π.r2. H
V = 1/3 π. 9. 4
V = 12 π m3
Understand more about the Pythagorean theorem.
Cone Trunk Volume
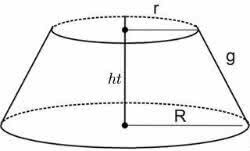
If we cut the cone in two parts, we will have the part that contains the vertex and the part that contains the base.
The trunk of the cone is the widest part of the cone, that is, the geometric solid that contains the base of the figure. It does not include the part that contains the vertex.
Thus, to calculate the volume of the trunk of the cone, the expression is used:
V = π.h/3. (R2 + R. r+r2)
Where:
V: cone trunk volume
π: constant equivalent to approximately 3.14
h: height
R: radius of larger base
r: radius of the smallest base
Example: Solved Exercise
Find the trunk of the cone whose radius of the largest base measures 20 cm, the radius of the smallest base measures 10 cm, and the height is 12 cm.
Resolution
To find the volume of the trunk of the cone, just put the values in the formula:
R: 20 cm
r: 10 cm
h: 12 cm
V = π.h/3. (R2 + R. r+r2)
V = π.12/3. (400 + 200 + 100)
V = 4п. 700
V = 2800 π cm3
Continue your search. Read the articles:
- Cone
- Cone Area
- Spatial Geometry
Entrance Exam Exercises with Feedback
1. (Cefet- SC) Given a cylinder-shaped cup and a conical-shaped cup of the same base and height. If I completely fill the conical cup with water and pour all that water into the cylindrical cup, how many times do I have to do this to completely fill this cup?
a) Only once.
b) Twice.
c) Three times.
d) Once and a half.
e) It is impossible to know, as the volume of each solid is not known.
Alternative c
2. (PUC-MG) A sand mound has the shape of a straight circular cone, with volume V= 4пm3. If the radius of the base is equal to two thirds of the height of this cone, it can be said that the measure of the height of the sand pile, in meters, is:
a) 2
b) 3
c) 4
d) 5
Alternative b
3. (PUC-RS) The radius of the base of a straight circular cone and the edge of the base of a regular quadrangular pyramid have the same measurement. Knowing that their heights measure 4 cm, then the ratio between the volume of the cone and the pyramid is:
to 1
b) 4
c) 1/п
d) п
e) 3п
Alternative
4. (Cefet-PR) The radius of the base of a straight circular cone measures 3 m and the perimeter of its meridian section measures 16 m. The volume of this cone measures:
a) 8п m3
b) 10п m3
c) 14п m3
d) 12п m3
e) 36п m3
Alternative
5. (UF-GO) The earth removed in the excavation of a semicircular pool with a radius of 6 m and 1.25 m in depth was heaped in the form of a straight circular cone, on a flat horizontal surface. Assume that the cone's generatrix makes an angle of 60° with the vertical and that the soil removed has a volume 20% greater than the volume of the pool. Under these conditions, the height of the cone, in meters, is:
a) 2.0
b) 2.8
c) 3.0
d) 3.8
e) 4.0
Alternative c