Geometric solids are three-dimensional objects, have width, length and height, and can be classified between polyhedra and not polyhedra (round bodies).
The main elements of a solid are: faces, edges and vertices. Each solid has its spatial representation and its flat representation (geometric solid flat pattern).
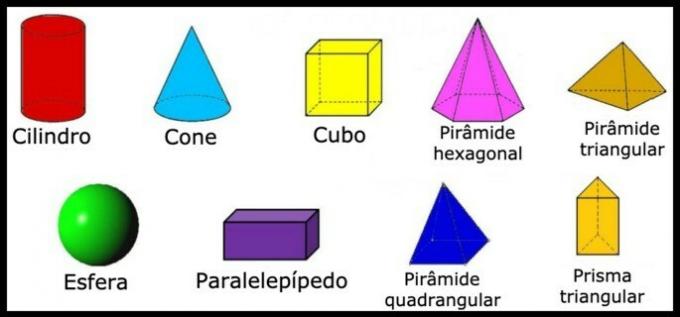
The names of geometric solids are generally given from their determining characteristic. Whether in relation to the number of faces that compose it, or as a reference to objects known in everyday life.
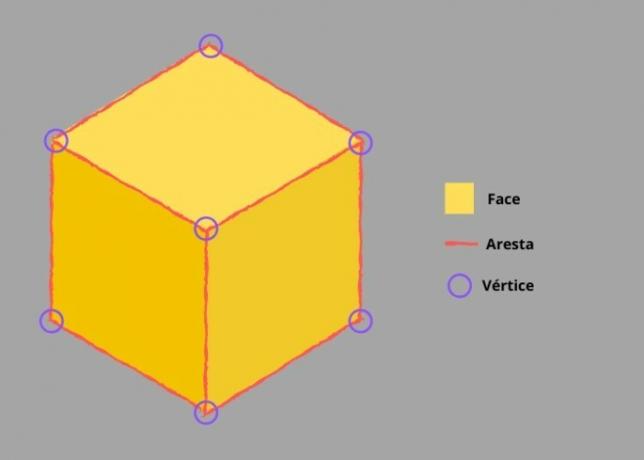
Geometric solids are composed of three fundamental elements:
- Faces - each of the faces of the solid.
- Edges - Lines that join the sides of the solid.
- Vertices - point of joining of edges.
The classification of solids is related to the number of sides and the polygon of its base. The most common solids worked on in geometry are regular solids.
See too: Spatial Geometry.
Pyramids
Pyramids are polyhedra characterized by having a polygonal base in the plane and only one vertex out of the plane. Its name is represented by the base polygon, the most common examples are:
- triangular pyramid;
- square pyramid;
- quadrangular pyramid;
- pentagonal pyramid;
- hexagonal pyramid.
Pyramid volume formula:
V = 1/3 Ab.h
- V: volume of the pyramid
- Ab: Base area
- h: height
See too:
- Pyramid volume
Prisms
You prisms are characterized by being polyhedra with two congruent and parallel bases, in addition to the flat lateral faces (parallelograms). The most common examples are:
- triangular prism;
- cube;
- paving stone;
- pentagonal prism;
- hexagonal prism.
Prism volume formula:
V = Ab.h
- Ab: base area
- H: height
See too: Prism volume.
Platonic Solids
Platonic solids are regular polyhedra whose faces are formed by regular and congruent polygons.
The equilateral triangular prism (4 faces, 6 edges and 4 vertices) and the cube (6 faces, 12 edges and 8 vertices) are platonic solids, besides them there are others like:
- octahedron (8 faces, 12 edges and 6 vertices);
- dodecahedron (12 faces, 30 edges and 20 vertices);
- icosahedron (20 faces, 30 edges and 12 vertices).
See too: Polyhedron.
Non-Polyhedra
The so-called non-polyhedra are geometric solids that have at least one curved surface as a fundamental characteristic.
round bodies
Among round bodies, geometric solids that have a curved surface, the main examples are:
-
Ball - continuous curved surface equidistant from a center.
Sphere volume ⇒ Ve = 4.π.r3/3 -
Cylinder - circular bases joined by a circular surface of the same diameter.
Cylinder volume ⇒ V = Ab.h or V = π.r2.h -
Cone - pyramid with a circular base.
Cone volume ⇒ V = 1/3 п.r2. H
Planning of Geometric Solids
The flat pattern is the representation of a geometric solid (three-dimensional) in a plane (two-dimensional). You should think about the unfolding of its edges and the shape that the object takes on the plane. For this, the number of faces and edges must be taken into account.
The same solid can have different forms of planning.