Parallelogram area: how to calculate?

THE parallelogram area it is related to the measure of the surface of this flat figure.

Remember that the parallelogram is a quadrilateral that has four congruent opposite sides (same size). In this figure, the opposite sides are parallel.

The parallelogram is a polygon (flat and closed figure) that has four internal and external angles. The sum of the internal or external angles is 360°.

Area formula

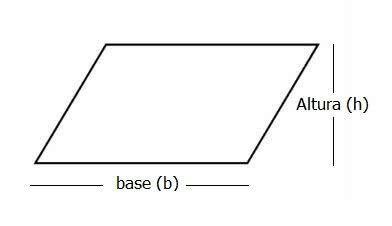
To calculate the measure of the parallelogram area, multiply the base value (b) by the height (h). So the formula is:

A = b.h

Complement your research by reading the articles:

• Parallelogram
• Polygon Area
• Polygons
• plane geometry

Stay tuned!

The perimeter of a flat figure, different from its area, corresponds to the sum of all the side measurements. Therefore, in the case of the parallelogram, the perimeter is given by the formula:

P = 2 (a+b)

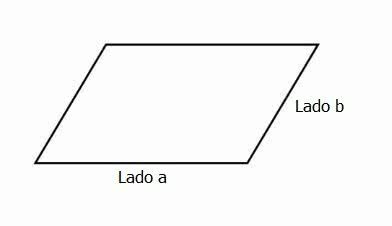
Where,

P: perimeter
The and B: two-sided lengths

Observation!

The area value is usually given in cm² (square centimeter), m² (square meter) or km² (square kilometer).

The perimeter will always be the simple unit of measurement, that is, it is given in cm (centimeter), m (meter) or Km (kilometer). This is because to find the area, the values ​​are multiplied and the values ​​are added to the perimeter.

Read more about the topic in the articles:

• Area and Perimeter
• Perimeters of Flat Figures

Did you know?

Parallelograms are defined as quadrilaterals of equal sides and parallel opposite sides. Thus, the square, rectangle and rhombus are also parallelograms.

See also articles on flat figure areas:

• Diamond Area
• Triangle Area
• Square Area
• Rectangle Area
• Trapeze Area
• Circle Area
• Flat Figure Areas

Solved Exercises

1. Calculate the area of ​​a parallelogram with a height of 28 cm and a base of 12 cm.

See Answer

A = b.h
A = 12. 28
H = 336 cm²

2. If a parallelogram has two 45° internal angles. What will be the value of the other two?

a) 45° and 90°
b) 120° and 45°
c) 130° and 140°
d) 136th and 240th
e) 90° and 75°

See Answer

Alternative c

If the sum of the internal angles of a parallelogram is 360°, to obtain the answer we must add the angles (in addition to the 90 already indicated in the statement).

3. Calculate the area of ​​a parallelogram where two consecutive sides measure 6 m and 10 m respectively, and form an angle of 45°.

See Answer

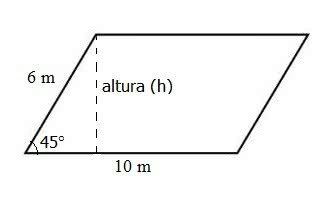
As we don't have the height measurement, we have to find this value first.

Thus, according to the figure, when we plot the height it forms a right triangle with a right angle of 90°.

Remember that the right triangle is formed by the hypotenuse (opposite the right angle) and two sides (opposite and adjacent). Here, we have to use the sine, cosine or tangent value of the 45° angle.

However, we have to remember that the sine is opposite side/hypotenuse; cosine is adjacent breast/hypotenuse; and the tangent is opposite side/adjacent side. Thus, in the figure we use the sine value of 45°.

Soon:

Without 45° = √2/2 = h/6
h = 3√2

After finding the height value we can calculate the parallelogram area:

A = b. H
A = 10. 3√2
A = 30√2 m²

Learn more about the topic:

• Pythagorean theorem
• Triangles Similarity - Exercises
• law of sins
• Cosine Law.