O slope, also called slope of a straight, determines the slope of a straight line.
Formulas
To calculate the slope of a straight line, use the following formula:
m = tg α
Being m a real number and α the angle of inclination of the straight line.
Attention!
- When the angle is equal to 0º: m = tg 0 = 0
- when the angle α is acute (less than 90º): m = tg α > 0
- when the angle α is straight (90º): it is not possible to calculate the slope because there is no tangent of 90º
- when the angle α is obtuse (greater than 90º): m = tg α
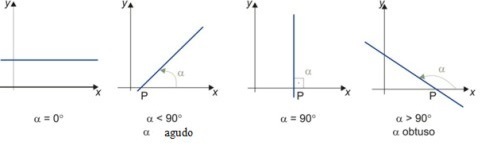
Representation of straight lines and their angles
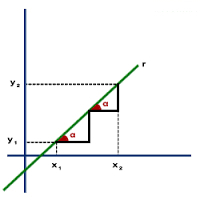
To calculate the slope of a line from two points we must divide the variation between the axes x and y:
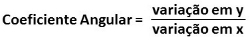
A straight line that passes through A (xTheyyThe) and B (xByyB) we have the relationship:
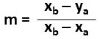
This relationship can be written as follows:

Where,
yy: represents the difference between the ordinates of A and B
Δx: represents the difference between the abscissa of A and B
Example:
To better understand, let's calculate the slope of the line that passes through A (– 5; 4) and B (3.2):
m = Δy/Δx
m = 4 – 2 / –5 – 3
m = 2/–8
m = -1/4
This value refers to the calculation of the difference of THE for B.
Likewise, we could calculate the difference of B for THE and the value would be the same:
m = Δy/Δx
m = 2 – 4 / –3 –(– 5)
m = –2/8
m = -1/4
Angular and Linear Coefficient
In studies of first-degree functions, we calculate the angular and linear coefficients of the straight line.
Remember that the first-degree function is represented as follows:
f (x) = ax + b
Where The and B are real numbers and a≠0.
As we saw above, the slope is given by the value of the tangent of the angle that the line forms with the axis of x.
The linear coefficient is the one that cuts the axis y of the Cartesian plane. In the representation of the first degree function f (x) = ax + b we have:
The: slope (x axis)
B: linear coefficient (y axis)
To learn more, read also:
- Line Equation
- Distance between two points
- Parallel Lines
- Perpendicular Lines
Entrance Exam Exercises with Feedback
1. (UFSC-2011) The straight line that passes through the origin and the midpoint of segment AB with A=(0.3) and B=(5.0) has which slope?
a) 3/5
b) 2/5
c) 3/2
d) 1
Alternative to: 3/5
2. (UDESC-2008) The sum of the slope and the linear coefficient of the straight line that passes through points A(1, 5) and B(4, 14) is:
a) 4
b) -5
c) 3
d) 2
e) 5
Alternative e: 5
Read too:
- Linear Function
- Affine Function
- straight
- angles