Check 10 solved questions from the last editions of Enem with the commented answers.
1. (Enem/2019) In a given year, the computers of the Federal Revenue of a country identified as inconsistent 20% of the income tax returns sent to it. A statement is classified as inconsistent when it presents some type of error or conflict in the information provided. These statements considered inconsistent were analyzed by the auditors, who found that 25% of them were fraudulent. It was also found that, among the statements that did not show inconsistencies, 6.25% were fraudulent.
What is the probability that, in that year, a taxpayer's declaration will be considered inconsistent, given that it was fraudulent?
a) 0.0500
b) 0.1000
c) 0.1125
d) 0.3125
e) 0.5000
Correct alternative: e) 0.5000.
Step 1: Determine the percentage of inconsistent statements that are fraudulent.
The number of declarations received that year by the federal revenue was not given, but according to the statement 20% of the total are inconsistent. Of the inconsistent portion, 25% were considered fraudulent. We then need to calculate percentage percentage, ie 25% of 20%.
Step 2: Determine the percentage of consistent claims that are fraudulent.
The rest of the statements, which represents 80%, were considered consistent. However, 6.25% of this portion was found to be fraudulent, that is:
Step 3: Calculate the probability of a statement being inconsistent and fraudulent.
The probability is given by:
Where, the probability of an event occurring, P(A), is given by the ratio between the number of cases that interest us, n(A), and the total number of possible cases, n().
As such, the probability of a statement being inconsistent and fraudulent is 50% or 0.5000.
See too: Probability
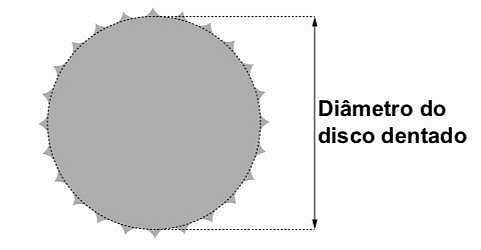
2. (Enem/2019) A cyclist wants to mount a gear system using two toothed discs on the back of his bicycle, called ratchets. The crown is the toothed disc that is moved by the bicycle's pedals, and the chain transmits this movement to the ratchets, which are positioned on the bicycle's rear wheel. The different gears are defined by the different diameters of the turnstiles, which are measured as shown in the figure.
The cyclist already has a ratchet with 7 cm in diameter and wants to include a second ratchet, so that as the chain pass through it, the bicycle advances 50% more than it would if the chain passed through the first ratchet, at each complete turn of the pedals.
The closest value to the measurement of the diameter of the second ratchet, in centimeters and to one decimal place, is
a) 2,3
b) 3.5
c) 4.7
d) 5.3
e) 10.5
Correct alternative: c) 4.7.
Note how the ratchet and crown are positioned on the bicycle.
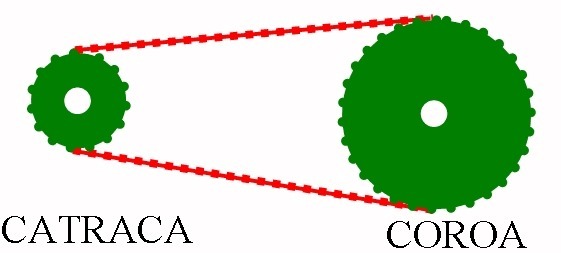
When the bicycle pedals move, the crown rotates and the movement is transmitted to the ratchet via the chain.
Because it is smaller, a turn of the crown makes the ratchet make more turns. If, for example, the ratchet is one-quarter the size of the crown, it means that a rotation of the crown will cause the ratchet to rotate four times more.
As the turnstile is located on the wheel, the smaller the turnstile used, the greater the speed reached and, consequently, the greater the distance covered. Therefore, ratchet diameter and distance traveled are inversely proportional quantities.
One of 7 cm has already been chosen and it is intended to advance 50% more with the bicycle, that is, the distance covered (d) plus 0.5 d (which represents 50%). Therefore, the new distance that must be reached is 1.5 d.
| Travelled distance | Ratchet Diameter |
| d | 7 cm |
| 1.5 d | x |
Since the proportionality between the magnitudes is inverse, we must invert the magnitude of the ratchet diameter and perform the calculation with the rule of three.
As the wheel and ratchet are interconnected, the movement performed on the pedal is transmitted to the crown and moves the 4.7 cm ratchet, making the bicycle advance 50% more.
See too: Simple and compound rule of three
3. (Enem/2019) To build a swimming pool, whose total internal surface area is equal to 40 m², a construction company presented the following budget:
- R$ 10 000.00 for the elaboration of the project;
- BRL 40,000.00 for fixed costs;
- R$ 2,500.00 per square meter for the construction of the indoor pool area.
After submitting the budget, this company decided to reduce the project preparation amount by 50%, but recalculated the value per square meter for the construction of the internal area of the pool, concluding that there is a need to increase it by 25%.
In addition, the construction company intends to give a discount on fixed costs, so that the new budget amount is reduced by 10% in relation to the initial total.
The percentage of discount that the construction company must grant on fixed costs is
a) 23.3%
b) 25.0%
c) 50.0%
d) 87.5%
e) 100.0%
Correct alternative: d) 87.5%.
1st step: calculate the initial investment value.
| Budget | Value |
| Project elaboration | 10 000,00 |
| fixed costs | 40 000,00 |
| Construction of the 40 m internal area2 the pool. | 40 x 2 500.00 |
2nd step: Calculate the project preparation value after the 50% reduction
3rd step: Calculate the square meter value of the pool after a 25% increase.
Step 4: Calculate the discount applied to fixed costs to reduce the initial budget amount by 10%.
With the application of the 87.5% discount, the fixed costs will go from R$ 40 000 to R$ 5 000 so that the final amount paid is R$ 135 000.
See too: How to calculate percentage?
4. (Enem/2018) A communication company has the task of preparing advertising material for a shipyard to publicize a new ship, equipped with a 15 m high crane and a 90 m high mat length. In the design of this ship, the representation of the crane must have its height between 0.5 cm and 1 cm, while the mat must have a length greater than 4 cm. All drawing should be done in a 1: X scale.
Possible values for X are just
a) X > 1500
b) X c) 1500 d) 1500 e) 2 250
Correct alternative: c) 1500
To resolve this issue, the distance in the drawing and the actual distance must be in the same unit.
The height of a crane is 15 m, which corresponds to 1500 cm, and the length of 90 m is the same as 9000 cm.
The relationship on a scale is given as follows:
Where,
And is the scale
d is the distance in the drawing
D is real distance
1st step: Find the values for X according to the height of the crane.
The scale should be 1: X, so as the height of the crane in the drawing should be between 0.5 cm and 1 cm, we have
Therefore, the value of X must be between 1500 and 3000, that is, 1500
2nd step: Find the value of X according to the length of the crane.
3rd step: Interpret the results.
The statement of the question says that the mat must have a length greater than 4 cm. Using scale 1: 3000 the length of the mat in the drawing would be 3 cm. As the length would be shorter than recommended, this scale cannot be used.
According to the measurements observed, to respect the material elaboration limits, we have that the value of X must be between 1500
5. (Enem/2018) With the advancement in computer science, we are close to the time when the number of transistors in the processor a personal computer will be of the same order of magnitude as the number of neurons in a human brain, which is on the order of 100 billion.
One of the determining quantities for a processor's performance is the transistor density, which is the number of transistors per square centimeter. In 1986, a company manufactured a processor containing 100,000 transistors distributed over 0.25 cm² of area. Since then, the number of transistors per square centimeter you can put on a processor has doubled every two years (Moore's Law).
Available at: www.pocket-lint.com. Accessed on: 1 Dec. 2017 (adapted).
Consider 0.30 as an approximation for
In what year did the company reach or will it reach the density of 100 billion transistors?
a) 1999
b) 2002
c) 2022
d) 2026
e) 2146
Correct alternative: c) 2022.
Step 1: Calculate the transistor density in 1986 in number of transistors per square centimeter.
2nd step: write the function that describes the growth.
If the transistor density doubles every two years the growth is exponential. The goal is to reach 100 billion, that is, 100 000 000 000, which in the form of scientific notation is 10 x 1010.
3rd step: apply the logarithm to both sides of the function and find the value of t.
4th step: calculate the year that will reach 100 billion transistors.
See too: Logarithm
6. (Enem/2018) The types of silver commonly sold are 975, 950 and 925. This classification is made according to its purity. For example, 975 silver is the substance made up of 975 parts pure silver and 25 parts copper in 1000 parts of substance. 950 silver, on the other hand, is made up of 950 parts of pure silver and 50 parts of copper out of 1,000; and 925 silver is made up of 925 parts pure silver and 75 parts copper out of 1000. A goldsmith has 10 grams of 925 silver and wants to obtain 40 grams of 950 silver to produce a jewel.
Under these conditions, how many grams of silver and copper, respectively, should be fused with the 10 grams of 925 silver?
a) 29.25 and 0.75
b) 28.75 and 1.25
c) 28.50 and 1.50
d) 27.75 and 2.25
e) 25.00 and 5.00
Correct alternative: b) 28.75 and 1.25.
1st step: calculate the amount of 975 silver in 10 g of the material.
For every 1000 parts of 925 silver, 925 parts are silver and 75 parts are copper, that is, the material is composed of 92.5% silver and 7.5% copper.
For 10 g of material, the proportion will be:
The remainder, 0.75 g, is the amount of copper.
2nd step: calculate the amount of silver 950 in 40 g of the material.
For every 1000 parts of 950 silver, 950 parts are silver and 50 parts are copper, that is, the material is composed of 95% silver and 5% copper.
For 10 g of material, the proportion will be:
The remaining 2 g is the amount of copper.
3rd step: calculate the amount of silver and copper to melt and produce 40 g of silver 950.
7. (Enem/2017) Solar energy will supply part of the energy demand of the campus of a Brazilian university. The installation of solar panels in the parking area and on the roof of the pediatric hospital will be used in university facilities and also connected to the network of the electric company that distributes energy.
The project includes 100 m2 solar panels that will be installed in parking lots, producing electricity and providing shade for cars. About 300 m will be placed over the pediatric hospital.2 of panels, being 100 m2 to generate electricity used on campus, and 200 m2 for the generation of thermal energy, producing heating water used in the hospital's boilers.
Suppose that each square meter of solar panel for electrical energy generates a saving of 1 kWh per day and each square meter producing thermal energy saves 0.7 kWh per day for the University. In a second phase of the project, the area covered by solar panels that generate electricity will be increased by 75%. In this phase, the coverage area should also be expanded with panels for generating thermal energy.
Available in: http://agenciabrasil.ebc.com.br. Accessed on: 30 Oct. 2013 (adapted).
To obtain twice the amount of energy saved daily, compared to the first phase, the total area of panels that generate thermal energy, in square meters, should have the closest value in
a) 231.
b) 431.
c) 472.
d) 523.
e) 672.
Correct alternative: c) 472.
1st step: calculate the savings generated by panels for the production of electricity in the parking lot (100 m2) and in the pediatric hospital (100 m2).
2nd step: calculate the savings generated by panels for the production of thermal energy (200 m2).
Thus, the initial savings in the project are 340 kWh.
3rd step: calculate the electricity savings of the second phase of the project, which corresponds to 75% more.
Step 4: Calculate the total area of the thermal energy panels to get double the amount of energy saved daily.
8. (Enem/2017) A company specialized in swimming pool conservation uses a product for water treatment whose technical specifications suggest that 1.5 mL of this product be added for every 1,000 L of water from the pool. This company was hired to take care of a rectangular base pool, with a constant depth equal to 1.7 m, with width and length equal to 3 m and 5 m, respectively. The water level of this pool is kept 50 cm from the edge of the pool.
The amount of this product, in milliliter, that must be added to this pool in order to meet its technical specifications is
a) 11.25.
b) 27.00.
c) 28.80.
d) 32.25.
e) 49.50.
Correct alternative: b) 27.00.
1st step: calculate the pool volume based on depth, width and length data.
2nd step: calculate the amount of product that should be added to the pool.
9. (Enem/2016) Absolute density (d) is the ratio between the mass of a body and the volume it occupies. A teacher proposed to his class that students analyze the density of three bodies: dA, dB and dC. The students verified that body A had 1.5 times the mass of body B and that body B, in turn, had 3/4 the mass of body C. They also observed that the volume of body A was the same as that of body B and 20% larger than the volume of body C.
After the analysis, the students correctly ordered the densities of these bodies as follows
a) dB b) dB = dA c) dC d) dB e) dC
Correct alternative: a) dB
1st step: interpreting the utterance data.
Pastas:
Volumes:
2nd step: calculate densities with reference to body B.
According to the expressions for densities, we observe that the smallest one is dB, followed by dA and the largest one is dC.
See too: Density
10. (Enem/2016) Under the guidance of a foreman, João and Pedro worked on the renovation of a building. João carried out repairs to the hydraulic part on floors 1, 3, 5, 7, and so on, every two floors. Pedro worked on the electrical part on floors 1, 4, 7, 10, and so on, every three floors. Coincidentally, they finished their work on the top floor. Upon completion of the renovation, the foreman informed, in his report, the number of floors in the building. It is known that, during the execution of the work, on exactly 20 floors, repairs were made to the hydraulic and electrical parts by João and Pedro.
What is the number of floors in this building?
a) 40
b) 60
c) 100
d) 115
e) 120
Correct alternative: d) 115.
1st step: interpret the question data.
John performs repairs at intervals of 2. (1,3,5,7,9,11,13...)
Pedro works at intervals of 3 (1,4,7,10,13,16...)
They meet every 6 floors (1,7,13...)
2nd step: write the arithmetic progression equation knowing that the last floor is the twentieth.
See too: arithmetic progression
Don't stop there. We believe these texts will be very useful in your studies:
- Mathematics in Enem
- Mathematics Quiz and its Technologies
- Natural Sciences and its Technologies
- Quiz Science of Nature and Its Technologies
- Enem Simulation: 20 questions that fell on the test
- Enem questions: 30 questions that fell on the test