The geometric mean is defined, for positive numbers, as the nth root of the product of no elements of a dataset.
Like the arithmetic mean, the geometric mean is also a measure of central tendency.
It is most often used on data that have successively increasing values.
Formula
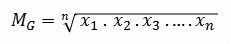
Where,
MG: geometric mean
n: number of dataset elements
x1, x2, x3,..., xno: data values
Example: What is the value of the geometric mean between the numbers 3, 8 and 9?
Since we have 3 values, we will calculate the cubic root of the product.
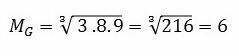
applications
As its name implies, geometric mean suggests geometric interpretations.
We can calculate the side of a square that has the same area as a rectangle, using the definition of geometric mean.
Example:
Knowing that the sides of a rectangle are 3 and 7 cm, find out how long the sides of a square with the same area measure.
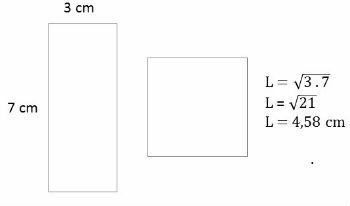
Another very frequent application is when we want to determine the average of values that have changed continuously, often used in situations involving finance.
Example:
An investment yields 5% in the first year, 7% in the second year and 6% in the third year. What is the average return on this investment?
To solve this problem we must find the growth factors.
- 1st year: 5% yield → 1.05 growth factor (100% + 5% = 105%)
- 2nd year: 7% yield → 1.07 growth factor (100% + 7% = 107%)
- 3rd year: 6% yield → 1.06 growth factor (100% + 6% = 106%)
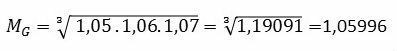
To find the average income we must do:
1,05996 - 1 = 0,05996
Thus, the average yield of this application, in the period considered, was approximately 6%.
To learn more, read also:
- Arithmetic average
- Average, Fashion and Median
- Statistic
- Standard deviation
- plane geometry
- Rectangle Area
- Square Area
Solved Exercises
1. What is the geometric mean of the numbers 2, 4, 6, 10 and 30?
Geometric Mean (Mg) = ⁵√2. 4. 6. 10. 30
MG = ⁵√2. 4. 6. 10. 30
MG = ⁵√14 400
MG = ⁵√14 400
MG = 6,79
2. Knowing the monthly and bimonthly grades of three students, calculate their geometric averages.
| Student | Monthly | bimonthly |
|---|---|---|
| THE | 4 | 6 |
| B | 7 | 7 |
| Ç | 3 | 5 |
Geometric Mean (MG) Student A = √4. 6
MG = √24
MG = 4,9
Geometric Mean (MG ) Student B = √7. 7
MG = √49
MG = 7
Geometric Mean (MG ) Student C = √3. 5
MG = √15
MG = 3,87