O Pascal's triangle it's a pretty old math tool. Throughout history, it has received several names, but the most adopted today are arithmetic triangle and Pascal's triangle. The second name is a tribute to the mathematician who made several contributions to the study of this triangle. means that the triangle was invented by him, but he was the one who made a deeper study of this tool.
From the properties of Pascal's triangle, it is possible to construct it logically. Also stands out your relationship with combinations studied in combinatorial analysis. The terms of the Pascal triangle also correspond to binomial coefficients and, therefore, it is very useful for calculating any Newton binomial.
Read too: Briot-Ruffini device - method for dividing polynomials
Construction of Pascal's triangle
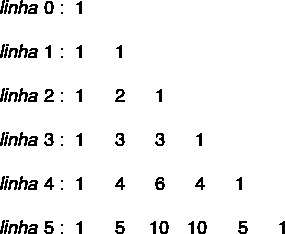
Pascal's triangle is produced from the result of the combinations, however there is a practical method that facilitates the way to build it. The first row and first column are counted as row zero and column zero.
We can use as many lines as needed in this construction, therefore the triangle can have infinite lines. The reasoning for the elaboration of the lines is always the same. Look:
We know that triangle terms are combinations, studied in combinatorial analysis. For replacing Pascal's triangle with numerical values, we know that the combinations of a number with zero and a number with itself are always equal to 1. Therefore, the first and last values are always 1.

To find the others, we start with line 2, since line 0 and line 1 are already complete. In line 2, to find the combination of 2 to 1, in the line above, that is, in line 1, let's add the term above it in the same column and the term above it in the previous column, as shown in the image:

After building line 2, it is possible to build line 3 performing the same procedure.

Continuing this procedure, we will find all the terms – in this case, up to line 5 – but it is possible to build as many lines as necessary.
Properties of Pascal's Triangle
There are some properties of Pascal's triangle, due to the regularity in its construction. These properties are useful for working with combinations, the construction of triangle lines itself, and the sum of lines, columns, and diagonals.
1st property
The first property was the one we used to build the triangle. So to find a term in Pascal's triangle, just add the term that is in the row above it and the same column with the term that is in the column and row before it. This property can be represented as follows:

This property is known as Stifel's relationship and it is important to facilitate the construction of the triangle and find the values of each of the lines.
Do not stop now... There's more after the advertising ;)
2nd property
The sum of all terms in a row is calculated by:
sno=2no, on what no is the line number.
Examples:

With this property, it is possible to know the sum of all terms on a line without necessarily having to construct Pascal's triangle. The sum of line 10, for example, can be calculated by 210 = 1024. Although not all terms are known, it is already possible to know the sum value of the entire line.
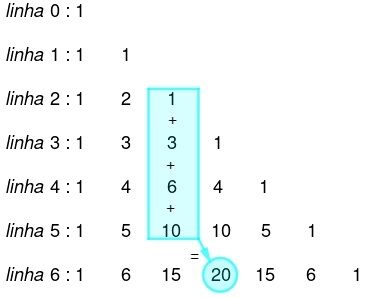
3rd property
The sum of terms that sequence from the beginning of a given column P up to a certain line no is the same as the term on the line n+1 back and column p+1 later, as shown below:
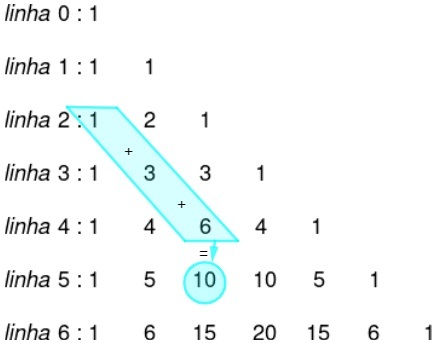
4th property
The sum of a diagonal that starts in column 0 and goes to the term in column p and row n is equal to the term in the same column (p), but in the row below (n+1), as shown in the image :
5th property
There is symmetry in the lines of Pascal's triangle. The first and second term are equal, the second and penultimate term are equal, and so on.
Example:
Line 6: 1615 20 156 1.
Note that the terms are equal two to two, except for the central term.
See too: Polynomial division: how to solve it?
Newton's binomial
We define Newton's binomial a power of one polynomial which has two terms. The calculation of a binomial is related to the Pascal triangle, which becomes a mechanism for calculating what we call binomial coefficients. To calculate a binomial, we use the following formula:

Note that the exponent value of The it decreases until in the last term it is equal to The0. We know that every number raised to 0 is equal to 1, hence the term The does not appear in the last term. Also note that the exponent of B begins with B0, soon B does not appear in the first term and increases until reaching Bno, in the last term.
Furthermore, the number that accompanies each of the terms is what we call a coefficient – in this case known as a binomial coefficient. To better understand how to solve this type of binomial, access our text: Newton's binomial.
binomial coefficient
The binomial coefficient is nothing more than the combination, which can be calculated using the formula:

However, to facilitate the calculation of Newton's binomial, it is essential to use the Pascal triangle, since it gives us the result of the combination faster.
Example:

To find the result of the binomial coefficient, let's find the values of row 5 of Pascal's triangle, which are {1,5,10,10,5,1}.
(x+y)5= 1x5+5x4y+10x3y2+ 10x2y3 + 5xy4+1y5
Simply put:
(x+y)5= x5+5x4y+10x3y2+ 10x2y3 + 5xy4+y5

solved exercises
Question 1 - The value of the expression below is?
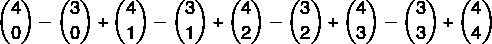
A) 8
B) 16
C) 2
D) 32
E) 24
Resolution
Alternative A.
Regrouping the positive and negative values, we have to:

Note that we are actually calculating the subtraction between line 4 and line 3 of Pascal's triangle. By property, we know that:
s4 = 24 = 16
s3= 23 = 8
16 – 8 = 8.
Question 2 - What is the value of the expression below?

A) 32
B) 28
C) 256
D) 24
E) 54
Resolution
Alternative B.
Note that we are adding the terms from column 1 of Pascal's triangle to row 7, then to the 3rd property, the value of this sum is equal to the term that occupies row 7+1 and column 1+1, that is, row 8, column 2. Since we only want one value, constructing the entire Pascal triangle is not convenient.

By Raul Rodrigues de Oliveira
Maths teacher