A sphere is a geometric solid formed by the 180° rotation of a circumference around your own central axis, also called axis of rotation.

Note that the ball it can also be defined by the 360° rotation of a semicircumference around its diameter. The following image on the left shows a semicircle it's yours diameter and, on the right, the sphere resulting from its revolution (turn).

Sphere Elements
Sectiongivesball: is a cut made in the sphere by a plane. It is the intersection between a sphere and a plane. Any intersection between the sphere and the plane generates a circle. If this plane passes through the center of the sphere, in addition to generating a circle with the same radius as the sphere, this circle will be as large as possible, called a maximum circle.

For cross sections, the list applies:
The2 = r2 + b2
- a is the radius of the circumference formed by the cross section;
- r is the radius of the sphere;
- B is the distance from the center of the sphere to the cross section.
Surfacespherical
: is the “shell” of the sphere. It can be obtained by 360° turning a semicircumference around its diameter. It is the part of the sphere used to calculate its area. For this calculation, the formula used is as follows:
A = 4πr2
*r is the radius of the sphere.
poles: the “highest” and “lowest” point of a sphere. These are the intersections between the diameter of the semicircle that was rotated and the resulting solid.
-
Parallel: is the circumference observed in the cross section of the sphere with respect to its axis of rotation.
Remember: a sphere's cross section is the section perpendicular to its axis of rotation.
Ecuador: It is the parallel whose cross section passes through the center of the sphere. Thus, it is the largest parallel and has a radius equal to the sphere.
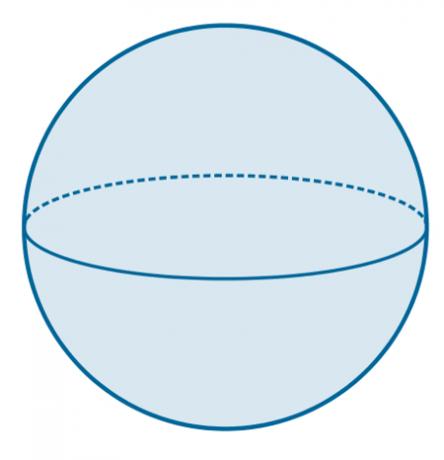
Example from Ecuador
Meridian: circumference resulting from the section of a sphere by a plane that contains its axis of rotation. In a way, we can say that parallels and meridians are perpendicular.

Examples of Meridians on a Sphere
Do not stop now... There's more after the advertising ;)
Wedgespherical
Imagine, in the definition of ball, that a semicircle does not complete the 360° turn. Let's say it takes a 30° turn. The figure will look something like the object in the following figure:

It is possible to calculate the volume of the spherical wedge using a basic rule of three or from a formula derived from that rule. To do so, just remember that the volume of the sphere is the result of the revolution of a semicircle around of its own diameter in 360° and that the spherical wedge is the result of the same revolution only in α degrees. Where V is the volume of the sphere and y is the volume of the spherical wedge, we will have:
V = y
360 α
Knowing that V = 4/3πr3, we will have:
4/3πr3 = y
360 α
360y = α4πr3
3
y = α4πr3
3·360
y = r3
270
spindlespherical
It is equivalent to the spherical wedge, but for a semicircumference. An example of a spherical spindle can be found in the figure below.

We can also calculate the spherical spindle area using a rule of three. To do this, remember that the complete spherical surface area is the result of a 360° revolution of a circle and that the spindle area is a revolution in α degrees of a circle. Since the complete surface area is A = 4πr2, the spherical spindle area is x and can be calculated as follows:
4πr2= x
360 α
Solving the equation, we will have:
360x = α4πr2
x = 4απr2
360
x = r2
90
Example
Calculate the area and volume of a part of the orange, knowing that the radius of the sphere of the orange is 4 centimeters and that the angle of that part is 90°.
To calculate the volume, we use the given formula or rule of three:
y = r3
270
y = 90·3,14·43
270
y = 282,6·64
270
y = 18086,4
270
y = 67 cm3
To calculate the area, just use the corresponding formula.
x = r2
90
x = 90·3,14·42
90
x = 282,6·16
90
x = 4521,6
90
x = 50.24 cm2
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "Elements of a Sphere"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/elementos-uma-esfera.htm. Accessed on June 27, 2021.
radian, angle, degree, circle, arc, arc of circle, transformation from degree to radian, Definition of radian, angle measure, arc measure, circumference length in radian, length of circumference.


