Pyramid Volume Calculation: formula and exercises

O pyramid volume corresponds to the total capacity of this geometric figure.

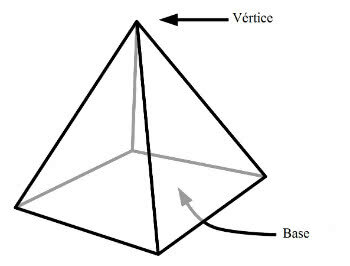
Remember that the pyramid is a geometric solid with a polygonal base. The apex of the pyramid represents the point farthest from its base.

Thus, all vertices of this figure are in the base plane. The height of the pyramid is calculated by the distance between the vertex and its base.

Regarding the base, note that it can be triangular, pentagonal, square, rectangular or parallelogram.

Formula: How to Calculate?

To calculate the volume of the pyramid, the following formula is used:

V = 1/3 A_B.H

Where,

V: volume of the pyramid
THE_B: base area
H: height

Solved Exercises

1. Determine the volume of a regular hexagonal pyramid with a height of 30 cm and a base edge of 20 cm.

Resolution:

First, we have to find the area at the base of this pyramid. In this example, it is a regular hexagon of side l = 20 cm. Soon,

THE_B = 6. there²√3/4
THE_B = 6. 20²√3/4
THE_B = 600√3 cm²

Once this is done, we can substitute the base area value in the volume formula:

V = 1/3 A_B.H
V = 1/3. 600√3. 30
V = 6000√3 cm³

2. What is the volume of a regular pyramid 9 m high with a square base with a perimeter of 8 m?

Resolution:

To solve this problem, we have to be aware of the concept of perimeter. It is the sum of all sides of a figure. Since it is a square, we have that each side has a measure of 2 m.

So, we can find the base area:

THE_B = 2² = 4 m

Once that's done, let's replace the value in the pyramid volume formula:

V = 1/3 A_B.H
V = 1/3 4. 9
V = 1/3. 36
V = 36/3
V = 12 m³

Entrance Exam Exercises with Feedback

1. (Vunesp) The mayor of a city intends to place a mast with a flag, which will be supported on a pyramid with a square base made of solid concrete, as shown The figure.

Knowing that the edge of the base of the pyramid will be 3 m and that the height of the pyramid will be 4 m, the concrete volume (in m³) required for the construction of the pyramid will be:

a) 36
b) 27
c) 18
d) 12
e) 4

See Answer

Alternative d: 12

2. (Unifor-CE) A regular pyramid is 6√3 cm high and the base edge measures 8 cm. If the internal angles of the base and all sides of this pyramid add up to 1800°, its volume, in cubic centimeters, is:

a) 576
b) 576√3
c) 1728
d) 1728√3
e) 3456

See Answer

Alternative to: 576

3. (Unirio-RJ) The lateral edges of a straight pyramid measure 15 cm, and its base is a square whose sides measure 18 cm. The height of this pyramid, in cm, is equal to:

a) 2√7
b) 3√7
c) 4√7
d) 5.7

See Answer

Alternative b: 3√ 7

read more:

• Pyramid
• Polyhedron
• Geometric solids
• Spatial Geometry
• Math Formulas