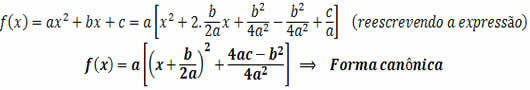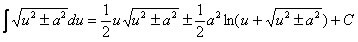At straight and the plans are primitive geometric figures in the geometry. This means that they have no definition, but are of great use and importance for other geometric figures. When we compare to position of a straight ordinary flat, we have three possibilities of positions. We will explain each of these possibilities below.
Line contained in the plane
We say that the straight r is contained in the α plane when all points on this line are points on the plane as well. Thus, we can say that when two points on a line belong to a plane, that line is contained in that plane. Another important detail: we can also say that the plane contains the straight line.

Example of a plane containing all points on a line
Line and plane competing
One straight r is called competitor to the α plane when the two geometric figures have only one point in common. It is also possible to say that straight and flat they are concurrent when the line touches, cuts or intersects the plane at just one point. When this happens, it can be said that the line is drying to the plan.
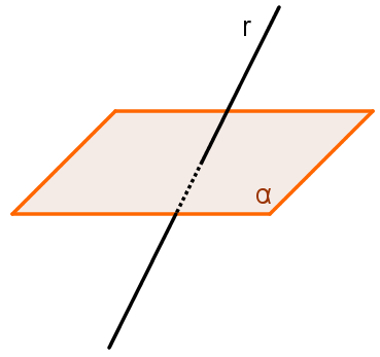
Example of secant straight to plane
Attention: it is not possible for a straight line to touch the plane at two points and not belong to it. This would only happen in the case of straight lines that make curves, however, these lines do not exist.
Straight and perpendicular plane
This is not an exclusive possibility of positionrelativein betweenstraightandflat, but it is a case of great importance. We say that a line r and a plane α are perpendicular when every line, which passes through the intersection point A of the line r with the plane α, is perpendicular to r.

Example of a plane whose lines passing through A are perpendicular to r
However, if it is possible to find two straight lines that pass through A, perpendicular each other and perpendicular to r, so r is perpendicular to α.
Parallel straight and plane
THE straight r is parallel to the α plane when the two figures have no common point. To check whether a line r is parallel to a plane α, just find a line contained in that plane that is parallel to straight r.

Example of a line r parallel to a line s contained in the plane
By Luiz Paulo Moreira
Graduated in Mathematics
Related video lesson: