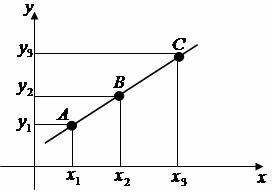
To determine the general equation of a line we use the concepts related to matrices. In determining the equation in the form ax + by + c = 0 we apply the Sarrus rule used to obtain the discriminant of a square matrix of order 3 x 3. In order to use a matrix in this determination of the feral equation, we must have at least two ordered pairs (x, y) of the possible aligned points, through which the line will pass. Note the general matrix of the general equation determination:

In the matrix we have the ordered pairs that must be informed: (x1y1) and (x2y2) and a generic point represented by the pair (x, y). Note that the 3rd column of the matrix is completed with the digit 1. Let's apply these concepts to obtain the general equation of the straight line that passes through points A(1, 2) and B(3,8), see:
Point A we have that: x1 = 1 and y1 = 2
Point B we have that: x2 = 3 and y2 = 8
Generic point C represented by ordered pair (x, y)
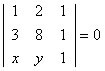
Calculating the determinant of a square matrix by applying Sarrus' rule means:
1st step: repeat the 1st and 2nd column of the matrix.
2nd step: add the products of the terms of the main diagonal.
3rd step: add the products of the terms of the secondary diagonal.
Step 4: Subtract the sum total of the main diagonal terms from the minor diagonal terms.
Do not stop now... There's more after the advertising ;)
Observe all steps in solving the dot matrix of the line:

[(1 * 8 * 1) + (2 * 1 *x) + (1 * 3 * y)] – [(2 * 3 * 1) + (1 * 1 * y) + (1 * 8 * x) ] = 0
[8 + 2x + 3y] - [6 + y + 8x] = 0
8 + 2x + 3y – 6 – y – 8x = 0
2x – 8x + 3y – y + 8 – 6 = 0
–6x + 2y + 2 = 0
Points A(1, 2) and B(3,8) belong to the following general equation of the line: –6x + 2y + 2 = 0.
Example 2
Let's determine the general equation of the line passing through the points: A(–1, 2) and B(–2, 5).
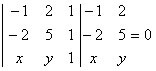
[– 5 + 2x + (–2y)] – [(– 4) + (– y) + 5x] = 0
[– 5 + 2x – 2y] – [– 4 – y + 5x] = 0
– 5 + 2x – 2y + 4 + y – 5x = 0
–3x –y – 1 = 0
The general equation of the line passing through points A(-1, 2) and B(-2, 5) is given by the expression: –3x – y – 1 = 0.
by Mark Noah
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "General Equation of the Line"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/equacao-geral-reta.htm. Accessed on June 29, 2021.