It is known that the quadratic function is determined by the following expression:
f(x)=ax2+bx+c
However, if we do some algebraic manipulations of the right side of this equality, through the process of completing squares.
(f(x)=ax2+bx+c (Placing the term The in evidence)
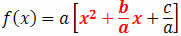
Note that the two highlighted parcels can be used for the square completion process:

So we just add and subtract the last term in our function f (x) (Process to complete squares).
Thus, completing the square in the function, we have:

Do not stop now... There's more after the advertising ;)
This expression can also be written as follows:

Calling from:

Note that:

So, another way to write the quadratic function canonically is:
f(x)=a(x-m)2+k
Let's do an example in which we should write any quadratic function:
f(x)=x2-3x-7
We must highlight the coefficients and determine the values of m and k:
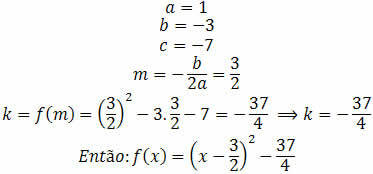
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Gabriel Alessandro de. "Quadratic function in canonical form"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/funcao-quadratica-na-forma-canonica.htm. Accessed on June 29, 2021.