The sum of the terms of a arithmetic progression (PA) can be obtained through the following formula:

In this formula, Sno represents the sum of terms, a1 it's the firstterm and theno it's the lastterm of the BP in question, n is the number of terms that will beadded together. To add the terms of an arithmetic progression, simply substitute the values in this formula.
Examples of summation of terms in a PA
Below are two examples of how to formula presented above can be used to obtain the sumFromterms of a PAN.
→ Example 1
Determine the sumFromterms of the following PA: (2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40).
To use the given formula, note that:
The1 = 2
Theno = 40
n = 20
This last data (number of terms) was obtained by counting the terms of the PA. Applying this data in the formula, we will have:

So, the sumFromterms of this PA is 420.
Note that this formula is only valid for arithmetic progressions who have a finite number of terms. If the PA is infinite, it will be necessary to limit the number of terms that will be added. When this occurs, it may be necessary to use other knowledge about AP to obtain the last term to be added.
See below an example of summing the terms of an infinite PA:
→ Example 2
Determine the sum of the first 50 terms of the following BP: (5, 10, 15, …).
Note that this PANis infinite, this is evidenced by the ellipses. The first term is 5, as is the BP ratio, as 10 – 5 = 5. Since we want to find the sum of the first 50 terms, the 50th term will be represented by a50. To find out its value, we can use the formula of general term of the PA:

In this formula, r is the BP ratio. Replacing the values given in the statement in this formula, we will have:
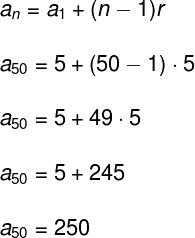
Knowing that the 50th term is 250, we can use the formula of sumFromterms to get the sum of the first 50 terms (S50) of this PA:
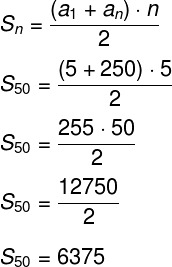
Gauss and the sum of terms of a PA
It is said that the German mathematician Gauss was the first to use an alternative method to addterms of a PAN, without needing to add term by term. Later, his idea of simplifying steps turned out to be the formula used to find the sum.
The story goes that, as a child, Gauss had a teacher who punished the whole class: adding up all the numbers from 1 to 100.
Gauss realized that adding the first number to the last, the second to the second to last, and so on gave the same result:
1 + 100 = 101
2 + 99 = 101
3 + 98 = 101
…
His biggest job was to observe that, as he was adding two numbers, he would find 50 results equal to 101, that is, the sum of all numbers from 1 to 100 could be found by doing 50 .101 = 5050.
The result obtained by Gauss can be checked through the formula of the sum of the terms of an AP. Watch:



