A line segment is nothing more than a part of a straight which has a starting point and an ending point, called "extremes”. In the following figure we have a line r, and the red part between points A and B is a line segment.
Note the straight line between points A and B
We can represent a line segment through two letters that characterize the points of its extremes with a line above them: 
or 
. They should be read as “Segment AB” or “Segment BA”. If two or more line segments have the same length, they are called congruent.
According to their position, the line segments can be further classified into consecutive segments,collinear segments or adjacent segments. If two straight segments are parallels, they will not be classified according to any of these three types of segments. Let's look at each of them:
Consecutive Segments
We say that two or more line segments are consecutive when they have a common point. Note the consecutive segments in the image below:
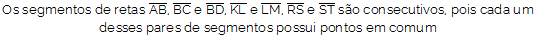
Do not stop now... There's more after the advertising ;)
Collinear Segments
Two or more line segments are called collinear when a single line passes through them or when they belong to the same line. an important axiom of Geometry guarantees that, through two distinct points, a single straight line passes. We can add that, for two distinct collinear line segments, it is only possible for a single line to be drawn. See some examples of collinear segments:
Adjacent Segments
If two straight line segments are consecutive and collinear simultaneously, that is, if, in addition to having points in common, they pass through a single line, they will be line segments. adjacent. We can conclude that all adjacent segments are necessarily consecutive and collinear. Let's look at some examples of adjacent segments:
By Amanda Gonçalves
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
RIBEIRO, Amanda Gonçalves. "Segments of Lines"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/segmentos-retas.htm. Accessed on June 27, 2021.
Point, line, Cartesian plane, slope, fundamental equation of the line, how to find the fundamental equation of the line, what is fundamental equation of the line, demonstration of the fundamental equation of the straight.
