THE square root is a math operation that accompanies all grade levels. This is a particular case of radiciation, in which the index of the radical is equal to 2, that is, it is the inverse operation of the powers of exponentequal to 2. When a positive number has exact square root, we say that this number is one perfect square.
Read too:Properties involving complex numbers
Definition and nomenclature of the elements of rooting
be Theand B two real numbers and no a natural number nonzero, so:

The = rooting
no = index
√ = radical
At square roots, as said, are a particular case of radiciation. When writing a squareroot, it is not necessary to spell out the index equal to two.
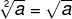
For the other types of roots, it is mandatory to place the index, that is, for n = 3, n = 4, n = 5 …, it is necessary to make explicit in the index of the radical the value of no.
Read too: Radical reduction at the same rate
Do not stop now... There's more after the advertising ;)
How to calculate a square root?
To calculate the square root of a real number, just follow the definition of rooting:

THE definition tells us that the square root of a real number The is the number B if and only if the number B squared equals the number The, that is, we have to imagine a number that, by square, result in the number inside the radical.
Examples:
√36 = 6, since 62 = 36
√ 121 = 11, because 112 = 121
Numbers that have a square root are called perfect squares. So, from the examples above, the numbers 36 and 121 are perfect squares. When the number is not a perfect square, it is necessary to perform the calculation of inexact roots.

Comments:
1. Realize, based on the definition of square root, what ever we look for a number that, when raised to the square, results in the number within the radical. In view of the potentiation properties, we know that a squared number is always positive. This leads us to conclude that it is not possible to extract square root of a negative number in the set of real numbers.
Example:
√ — 36 = ?
From the example above, we would have to imagine a number that, squared, would result in -36. In the set of real numbers, this is not impossible.
2. If the root is a relatively large number, which would make mental calculation impossible, just do the decomposition into primes and group whenever possible into powers of exponent two.
Example:
Let's determine the square root value of 441.
√441
To determine the root of 441, let's do the prime decomposition:
441 = 32. 72
Thus,
√441 = √32. 72
Now, applying the radiciation properties, we have to:
√441 = 3. 7 = 21
The number 21 squared equals 441.
Mind Map: Square Root

*To download the mind map in PDF, Click here!
Geometric interpretation of square root
Imagine a land with an area of 144 m2.

To determine how long the side of this square-shaped terrain is, we have to remember how to calculate its area.
square = 12
A represents the area value, and l is the side value.
As the area is worth 144 m2, We have to:
144=l2
Look at the equation above. Note that we need to find a number that, squared, equals 144, that is, we have the definition of square root! Then:
√144 = 12
The number 144 in factored form is:
144 = 22. 22. 32
So, we're going to have to:
√144 = √22. 22. 32
Lastly,
√144 = 2. 2. 3 = 12
Therefore, the land side measures 12 m.
solved exercises
1. Make a list of perfect squares from 1 to 100.
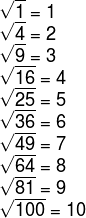
The perfect squares from 1 to 100 are: 1, 4, 9, 16, 25, 36, 49, 64, 81 and 100
2. Determine the square root of the number 1024.
√1024
To determine the root of 1024, let's do the decomposition into primes:
1024 = 22. 22. 22. 22. 22
Then,
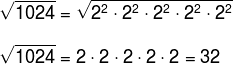
Considering the second equality with the properties of rooting already applied.
*Mental Map by Luiz Paulo Silva
Graduated in Mathematics
by Robson Luiz
Maths teacher


