With a point and an angle we can indicate and construct a straight line. And if the formed line is not vertical (vertical line is perpendicular to the Ox axis) with the point belonging to it plus its angular coefficient (slope angle tangent) it is possible to determine the fundamental equation of straight.
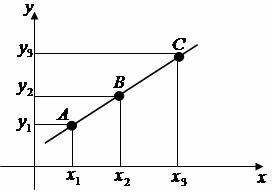
Considering a line r, the point C(x0y0) belonging to the line, its slope m and another generic point D(x, y) different from C. With two points belonging to the line r, we can calculate its slope.
m = y - y0
x - x0
m (x - x0) = y - y0
Therefore, the fundamental equation of the line will be determined by the following equation:
y-y0 = m (x - x0)
Example 1:
Find the fundamental equation of the line r that has the point A (0,-3/2) and slope equal to m = -2.
y-y0 = m (x - x0)
y – (-3/2) = - 2(x – 0)
y + 3/2 = -2x
2x - y - 3/2 = 0
Example 2:
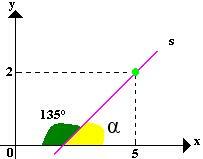
Obtain an equation for the line shown below:
To determine the fundamental equation of the line we need a point and the value of the slope. The point was given (5.2), the slope is the tangent of the angle α.
We will obtain the value of α with the difference 180° - 135° = 45°, then α = 45° and a tg 45° = 1.
y-y0 = m (x - x0)
y – 2 = 1 (x – 5)
y – 2 = x – 5
-x + y + 3 = 0
Do not stop now... There's more after the advertising ;)
by Danielle de Miranda
Graduated in Mathematics
Brazil School Team
Analytical Geometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
RAMOS, Danielle de Miranda. "Fundamental equation of the straight line"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/equacao-fundamental-reta.htm. Accessed on June 28, 2021.