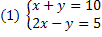One polygon is a geometric figure formed by straight segments. This figure is closed and none of these line segments are found except at its ends. when the polygon is convex, it is possible to discover the sum of your internal angles without having to measure them. This is done using a mathematical formula.
convex polygon
One polygon é convex when the line segment whose ends are points inside the polygon is entirely within it. In other words, some polygons they have a kind of “mouth” so that it is possible to choose two of their points and connect them by a straight segment that is not entirely inside the polygon. These are the calls noconvex.
Take a look at the image below which shows a polygonconvex on the left and a non-convex on the right.
Sum of internal angles
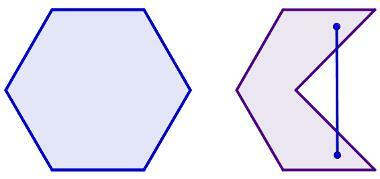
The sum of the interior angles of any triangle equals 180°. With that in mind, we can think about splitting the polygonsconvex in triangles. If a polygon can be divided into three triangles, for example, the sum of its interior angles equals 3 times 180.
To do so, it is necessary to create a division in which the sum From angles From triangles is equal to the sum of the angles of the polygons.
It is easy to see that if we choose a vertex of a polygon, its diagonals will form triangles that fulfill this prerequisite. Look at the image below:
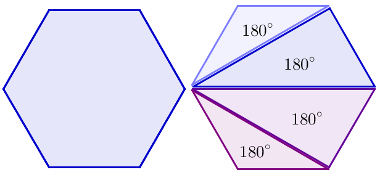
This figure is a hexagon. Note that, starting from the same vertex, it is possible to divide it into four triangles. For any figure, it will always be possible to find n – 3* diagonals starting from the same vertex and, consequently, n – 2* triangles will be formed in this process (*n = number of sides of the polygon).
As already said, the sum of the anglesinternalinapolygon is equal to the number of triangles formed within it multiplied by 180°. Therefore, the sum of the internal angles of a convex polygon is:
S = (n – 2) 180°
Examples:
What is the sum of the internal angles of a convex icosagon?
Icosagons are polygons that have 20 sides. The sum of the internal angles is:
S = (n – 2)180
S = (20 - 2)180
S = 18·180
S = 3280°
What is the measurement of each internal angle of a regular icosagon?
Regular polygons have congruent angles. So, already knowing that the sum of the internal angles of the icosagon is 3280°, each angle of it is equal to:
3280 = 162°
20
By Luiz Paulo Moreira
Graduated in Mathematics
Take the opportunity to check out our video classes on the subject: