In the study of circles, an important concept to be studied is that of tangent lines to a circle. In order to carry out this study, it is necessary to understand the relative positions of a point in relation to a circle. If you haven't studied something related to this topic, check out the article Relative positions between a point and a circle.
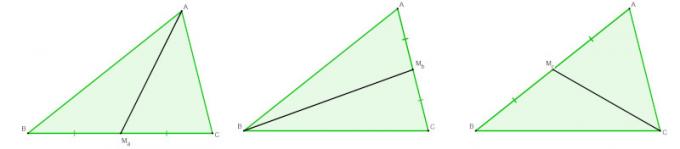
Observing the position of a point in relation to a circle, we can conclude some facts related to tangent lines. It is known that there are three relative positions from a point to a circle. For each position of this, we can conclude something about the tangent line that passes through that point.
• Point inside the circle: You cannot draw a tangent line through this point.
• Point belonging to the circle: through this point we can only have a tangent line, as it is the tangency point.
• Point outside the circle: from this point we can draw two lines tangent to the circle.
Therefore, to determine the equation of the line tangent to a circle through a given point, we must necessarily determine the relative position of that point. This position depends on the distance from the point to the center of the circle.
We must remember some important facts about analytic geometry:
• The shortest distance from a point to a line is a segment perpendicular to this line;
• The tangent line will always be perpendicular to the ray at its tangent point.
Relating the two previous facts, it can be stated that the distance from the tangent line to the center must be equal to the radius.
Therefore, to determine the equation of the tangent line, we must analyze the position of the point we will draw to the line and with that calculate the distance of the line that contains this point in relation to the center of the circumference.
For a better understanding of all these concepts, we will work with examples that need these reflections.
1) Determine the equation(s) of the line(s) tangent(s) to the given circle, drawn by the point P.
a) eq. circumference: x2+ y2 - 6x - 8y = 0 P (0.0)
Do not stop now... There's more after the advertising ;)
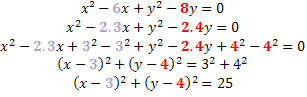
With that, we can extract the necessary information for our problem:
C(3,4), r=5.
We must now find the relative position of point P(0,0):

Therefore, point P is the tangency point.
Let's determine the equation of the straight line through point P.

In order to actually determine the equation of the line, we still need to find out what the slope of this line is. One of the facts we saw at the beginning of this article was the perpendicularity of the tangent line to the radius of the circle. Point P is a point of tangency, so the slope of the line that passes through point P and the center must be perpendicular to the tangent line. For this, we have a relationship between perpendicular slopes.

In other words, the product of the slopes of perpendicular lines is equal to -1.
To determine the slope of the PC segment, we must use the following expression:
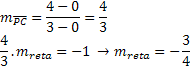
With that, we obtain the equation of the tangent line:

Another way to determine the value of m would be to calculate the distance from the center to the line. This distance is equal to the radius. Let's see:
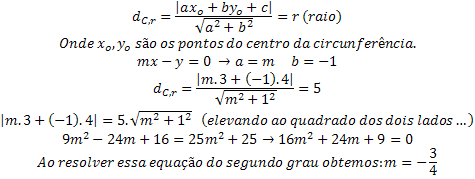
When the point is outside the circle, we should find the tangency point using the distance from the center of the circle to the tangent line, so we will determine the value of the angular coefficient of the tangent line, which, in turn, will determine the equation of the line tangent.
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Gabriel Alessandro de. "Tangance to the circumference"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/tangencia-circunferencia.htm. Accessed on June 29, 2021.