Linear systems consist of a set of linear equations that have a relationship between them. This relationship, in turn, occurs through the solution set of these equations. When we write two or more equations in a linear system, we are saying that the solutions of those equations must be equal. The values that the unknowns will assume to validate one of the equations must be the same for the others, that is, all the equations of this linear system must have the same solution set.
Therefore, we say that the set (a1, a2, a3, …, Theno) is the solution set of a linear system, if this is the solution of each of the linear system equations. Let's look at an example so that we can better understand this whole theory:
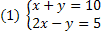
We have a system with two equations: in the first equation we can list several sets of solutions that satisfy this equation, however we must find, among these sets, one that also satisfies the second equation. Let's analyze the solution set (6.4):
• In the equation x + y = 10. S = {(6,4)}, that is, x = 6 and y = 4.
6 + 4 = 10 (True equality, this solution set satisfies the first equation)
• In the equation 2x – y = 5 (x = 6 and y = 4)
We will have: 2.6 - 4 = 5 -> 8 = 5 (False)
Do not stop now... There's more after the advertising ;)
This solution set does not satisfy the second equation, so we cannot say that this solution set is the solution of the linear system.
Let's look at the solution set (5.5). In this case, both equations will be satisfied with this set, so this is the solution set of the linear system (1).
However, note that, depending on the linear system, obtaining the solution set becomes complicated, just by mentally calculating the possible solutions of each equation. However, there are arithmetic methods for solving a linear system, and many have already been studied in elementary school. (Addition, Replacement, Comparison)
It will not always be possible to find a solution set that actually satisfies all the equations of a given system. Faced with this impasse, the need arose to analyze the possibilities for obtaining the solution set and with this made it possible to list 3 possibilities for classifying a linear system according to its solution set. This subject is covered in the article. Classification of a Linear System.
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team.
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Gabriel Alessandro de. "Solution of Linear Systems"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/sistema-lineares.htm. Accessed on June 29, 2021.


