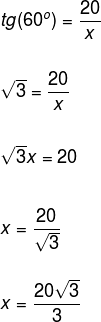O trianglerectangle has a angle internal measuring 90°, that is, it has a straight angle. The study of this type of triangle is very important, as it solves a series of practical problems using important tools, such as the Pythagorean theorem and the trigonometry.
Read too: Triangle classification - criteria and names
Main features of the right triangle
It is known that a triangle rectangle has only one internal angle measuring 90°. In addition to this feature, we can show that the other internal angles are smaller than 90°.
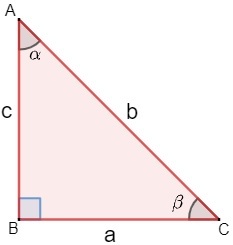
Consider the right triangle ABC:
We know that the sum of the interior angles of any triangle is equal to 180°, so we have:
α + β + 90° = 180°
α + β = 180° – 90°
α + β = 90°
Note that the sum of angles α and β gives 90°, this means that each of them must be less than 90°, as they cannot be equal to zero.
We must pay attention to the nomenclatures used from now on. O biggerside of the right triangle is called hypotenuse. The other sides are called peccaries.
In order to differentiate the legs from each other, let's establish the following rule: the leg that is facing at a certain angle, it will be called collaredopposite; and the leg that is next to from a certain angle, it will be called adjacent leg.
Therefore, in relation to angle α, we have:
a → opposite side
c → adjacent side
In relation to angle β, we have:
c → opposite side
a → adjacent side
Also note that the hypotenuse is always fixed, only the collared peccaries receive this differentiation in their nomenclature.
Pythagorean theorem
The right triangle has an important algebraic relationship that associates the measure of the hypotenuse with the measures of the legs. This relationship is known as the Pythagorean theorem, and, in fact, it is about the condition of existence of a right triangle, that is: if Pythagoras' theorem holds, the triangle is a rectangle, and vice versa.
"The square of the measure of the hypotenuse is equal to the sum of the squares of the measures of the legs."

Read more:Pythagoras Theorem – how to apply?
Trigonometry in the right triangle
We saw earlier that, in a right triangle, two inner angles are acute, that is, they have an amplitude less than 90°. Now let's determine the measurements of the sine, cosine and tangent from an acute angle.
- Sine of an angle is the ratio of the opposite side to the hypotenuse.
- cosine from an angle is the reason between the adjacent side and the hypotenuse.
- Tangent of an angle is the ratio of the opposite side to the adjacent side.

Now look at the sine, cosine and tangent values in a right triangle. Note that the sine, cosine and tangent values change depending on the reference angle:

Regarding angle α, we have:
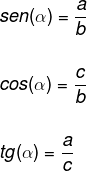
In relation to angle β, we have:


solved exercises
question 1 – (PUC-RS) A ball was kicked from point M, went up the ramp and went to point N, as shown in the figure:
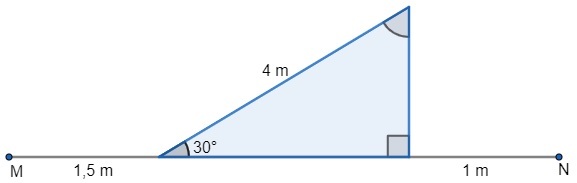
The distance between M and N is approximately:
a) 4.2 m
b) 4.5 m
c) 5.9 m
d) 6.5 m
e) 8.5 m
Resolution
Alternative c.
Note that, to determine the distance between points M and N, it is first necessary to find the measure of the leg. Next, see that we need to determine the measure of the leg adjacent to the 30° angle and that the hypotenuse has been given. The trigonometric relationship involving the adjacent side and hypotenuse is the cosine.

We know that √3 ≈ 1.7. Therefore, the ball travels:
1,5 + 2√3 +1
1,5 + 2(1,7) +1
1,5 + 3,4 + 1
4,9 + 1
5.9 m
Question 2 - (PUC-SP) What is the value of x in the following figure?

Resolution
Initially, let's determine the measure of the leg opposite the 30° angle. Thus:
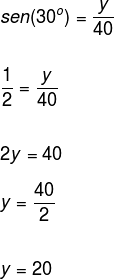
Viewing only the smallest triangle, see that we have the opposite side to the 60° angle and that we need to determine the value of the adjacent side. For this, we must use the tangent of the angle.