João lives in a house that has a large leisure area and a beautiful swimming pool.

One day he decided to ask his father how many liters of water are needed to fill the pool. João's father told his son that he would need to measure the dimensions of the pool, as only then would he calculate its capacity. To perform the measurement they used a measuring tape, which is an object suitable for measuring length. The measurements obtained were:
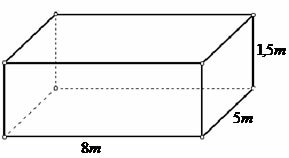
length = 8 meters
width = 5 meters
height or depth = 1.5 meters
The swimming pool at João's house has the shape of a parallelepiped and the capacity must be determined by multiplying the three dimensions.
Look:
length x width x depth
8 m x 5 m x 1.5 m = 60 m³ (sixty cubic meters)
The measure of 1 m³ (cubic meter) corresponds to 1000 liters. Therefore, 60 m³ equals the capacity of 60 000 liters.
The swimming pool at João's house has a capacity of 60 000 liters of water.
Now João wants to calculate the capacity of his house's water tank.

João and his father measured the dimensions and obtained the following values:
length: 1 meter
width: 1 meter
height or depth: 1 meter
In the water tank, all dimensions have equal measures, in this case, the geometric figure is called a cube, but the calculations are performed the same as for the parallelepiped, note:
length x width x depth
1 m x 1 m x 1 m = 1 m³ (one cubic meter)
The capacity of the water tank at João's house is 1000 liters.
Important: Other units of length can be used to calculate capacity. Therefore, note the relationship that exists between the volume and capacity measures.
1 cm³ (cubic centimeter) = 1 ml (milliliter)
1 dm³ (cubic decimeter) = 1 L (liter).
by Mark Noah
Mathematical
Related video lessons: