All equation which can be written in the form ax2 + bx + c = 0 is called second degree equation. In this case, the numbers represented by a, b, and c are real and called coefficients, and the coefficient a is always nonzero. The solutions of these equations, when they exist, can be obtained through the Bhaskara's formula. To use this resolution method, there are two steps:
1 – Replace the coefficients in the formula of discriminating (Δ), which is:
Δ = b2 – 4ac
2 – Replace coefficients and discriminant in formulainBhaskara, what is:
x = – b ± √∆
2nd
The formula of Bhaskara can be found applying another resolution process of the equationsofseconddegree about x2 + bx + c = 0. Details about this process can be found in the text square completion method.
Demonstration of Bhaskara's formula
To use the method of completing squares in demonstrating Bhaskara's formula, we must first divide the entire equation by the value of the coefficient a, as follows:
ax2 + bx + ç = 0
a a a a
x2 + bx + ç = 0
the a
x2 + bx = - ç
the a
After that, we'll divide b/a by 2 and we will raise the squared result. The portion obtained will be added in both members of the equation to form the perfect square trinomial on the left side of the equation. The result of this calculation will be:
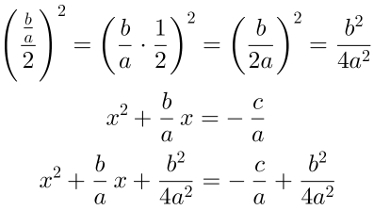
After that, we'll write the first member as a remarkable product and we'll simplify the second member as much as possible. Watch:
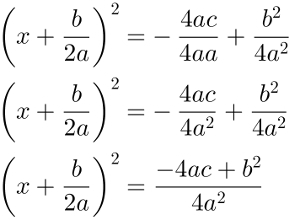
To go further in the calculation, we'll square root on both members of the equation and we'll simplify the result as much as possible:
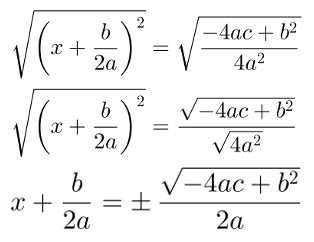
To finish the calculations, just put the term b/2a in the second member and simplify the result:
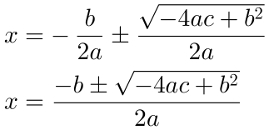
Note that the discriminating is found within the square root of the demonstration gives formulainBhaskara. It is only calculated separately for didactic reasons.
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/demonstracao-formula-bhaskara.htm
