As studied in the article of “Quadratic function in canonical form”, a quadratic function can be written in another way. In canonical form we can analyze the quadratic function in order to determine the maximum point or the minimum point.
Therefore, we have that the canonical form of a quadratic function is given as follows:
f(x)=a(x-m)2+k
In such a way that we must analyze the value of the coefficient The:
- If The > 0, the smallest value of the function f (x) is k = f (m)
- If The < 0, the greatest value of the function f (x) is k = f (m)
It is noteworthy that the value of m is given by the following expression:

Do not stop now... There's more after the advertising ;)
Let's look at the application of this concept.
Determine the maximum or minimum value of the following function:
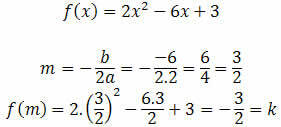
Therefore, the canonical form will be given by the following expression:

Since a > 0, the value k is the minimum point of the given function.
According to the theory seen above, if the value of the coefficient a were less than zero, we would have a maximum point instead of a minimum point.
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Roles - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Gabriel Alessandro de. "Maximum and Minimum of the function in canonical form"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/maximo-minimo-funcao-na-forma-canonica.htm. Accessed on June 29, 2021.