Roman numbers (Roman numerals)

You Roman numbers were the most used digit system in Europe during the Roman Empire, before being replaced by Indo-Arabic numerals, the system we currently use. the roman system had as symbols seven letters of the alphabet.

I → 1

V → 5

X → 10

L→ 50

Ç→ 100

D → 500

M → 1000

The other numbers are described by the repetition of these symbols, taking into account that there are also specific rules, depending on the position of their digits. This numbering system was useful for the daily life of the Romans, however, it is not very efficient, and that is why today we use the positional decimal system. There are still some representations in Roman numbers, for example, the centuries and topics of a particular law.

Read too: What are prime numbers?

Roman numbers are represented by letters of the Roman alphabet.

Roman numeral rules

Using the seven symbols, we can represent several numbers in the Roman numeral system, but for that, it is necessary to respect some rules relative to the positional value of the symbol.

To represent numbers using symbol combinations, when we have a larger letter on the left (that is, we write from largest to smallest letter) or when we have the repetition of the same symbol, the addition:

Examples:

a) III = 1 + 1 + 1 = 3

b) VI = 5 + 1 = 5

c) XVII = 10 + 5 + 1 + 1 = 17

d) MDCLX = 1000 + 500 + 100 + 50 + 10 = 1660

e) MCCII = 1000 + 100 + 100 + 2 = 1202

Do not stop now... There's more after the advertising ;)

To perform the sum, a symbol can be repeated up to three times. In Roman numerals, the symbol is not used in sequence four times to make sums. The exception is the symbol D, which represents 500, as if you have a symbol to represent 1000, which is M, the digit D will never appear twice in a number.

Now, when we represent a smaller digit à left of a larger digit, in this case, we carry out the subtraction between them.

Examples:

a) IV = 5 - 1 = 4

b) IX = 10 - 1 = 9

The digit I can only be used preceding V or X, and we don't use repetitions of it in this case. For example, to represent 3, we use III, as IIV does not exist in Roman numerals.

With the combination of these symbols, we can represent numbers like 14, 19, 24, 29.

a) XIV → 10 + 5 – 1 = 14

b) XIX → 10 + 10 – 1 = 19

c) XXIV → 10 + 10 + 5 – 1 = 24

d) XXIX → 10 + 10 + 10 – 1 = 29

e) XXXIV → 10 + 10 + 10 + 5 - 1 = 34

f) XXXIX → 10 + 10 + 10 - 1 = 39

Using the same idea, the letter X can precede the L and the C as subtraction, making it possible to represent numbers as:

a) XL → 50 – 10 = 40

b) XC → 100 – 10 = 90

There are no representations of the LC type, which, using this logic, would correspond to 100 – 50. The number 50 is represented by L, as we saw, so this representation would not make sense, so the L never será used before a letter representingand larger quantities.

The letter C can be used preceding the letters D and M, making it possible to represent numbers such as:

a) CD → 500 – 100 = 400

b) MC → 1 000 – 100 = 900

c) MCD → 1000 + 500 – 100 = 1400

d) MCM → 1000 + 1000 – 100 = 1900

e) DMARD → 1000 + 1000 + 500 – 100 = 2400

Using these previous rules, the largest number that can be formed is 3999 (MMMCMXCIX), as the sequence of four repeated symbols in the Roman system is not used, however, to represent larger numbers, use a slash above the digit:

Examples:

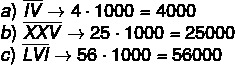
See too: Set of natural numbers - how is it formed?

Table with roman numbers

Numbers	Roman numbers
1	I
2	II
3	III
4	IV
5	V
6	SAW
7	VII
8	VIII
9	IX
10	X
11	XI
12	XII
13	XIII
14	XIV
15	XV
16	XVI
17	XVII
18	XVIII
19	XIX
20	XX
21	XXI
22	XXII
23	XXIII
24	XXIV
25	XXV
26	XXVI
27	XXVII
28	XXVIII
29	XXIX
30	XXX
31	XXXI
32	XXXII
33	XXXIII
34	XXXIV
35	XXXV
36	XXXVI
37	XXXVII
38	XXXVIII
39	XXXIX
40	XL
41	XLI
42	XLII
43	XLIII
44	XLIV
45	XLV
46	XLVI
47	XLVII
48	XLVIII
49	XIX
50	L
51	LI
52	LII
53	LIII
54	LIV
55	LV
56	LVI
57	LVII
58	LVIII
59	LIX
60	LX
61	LXI
62	LXII
63	LXIII
64	LXIV
65	LXV
66	LXVI
67	LXVII
68	LXVIII
69	LXIX
70	LXX
71	LXXI
72	LXXII
73	LXXIII
74	LXXIV
75	LXXV
76	LXXVI
77	LXXVII
78	LXXVIII
79	LXXIX
80	LXXX
81	LXXXI
82	LXXXII
83	LXXXIII
84	LXXXIV
85	LXXXV
86	LXXXVI
87	LXXXVII
88	LXXXVIII
89	LXXXIX
90	XC
91	XCI
92	XCII
93	XCIII
94	XCIV
95	XCV
96	XCVI
97	XCVII
98	XCVIII
99	XCIX
100	Ç
200	CC
300	CCC
400	CD
500	D
600	A.D
700	DCC
800	DCCC
900	CM
1000	M
1100	MC
1200	MCC
1300	MCCC
1400	MCD
1500	MD
1600	MDC
1700	MDCC
1800	MDCCC
1900	MCM
2000	MM
2100	MMC
2200	MMCC
2300	MMCCC
2400	DMARD
2500	MMD
2600	MMDC
2700	MMDCC
2800	MMDCCC
2900	MMCM
3000	MMM

Years in Roman numerals

Year	year in roman
1000	M
1100	MC
1200	MCC
1300	MCCC
1400	MCD
1500	MD
1600	MDC
1700	MDCC
1800	MDCCC
1900	MCM
1901	MCMI
1902	MCMII
1903	MCMIII
1904	MCMIV
1905	MCMV
1906	MCMVI
1907	MCMVII
1908	MCMVIII
1909	MCMIX
1910	MCMX
1911	MCMXI
1912	MCMXII
1913	MCMXIII
1914	MCMXIV
1915	MCMXV
1916	MCMXVI
1917	MCMXVII
1918	MCMXVIII
1919	MCMXIX
1920	MCMXX
1921	MCMXXI
1922	MCMXXII
1923	MCMXXIII
1924	MCMXXIV
1925	MCMXXV
1926	MCMXXVI
1927	MCMXXVII
1928	MCMXXVIII
1929	MCMXXIX
1930	MCMXXX
1931	MCMXXXI
1932	MCMXXXII
1933	MCMXXXIII
1934	MCMXXXIV
1935	MCMXXXV
1936	MCMXXXVI
1937	MCMXXXVII
1938	MCMXXXVIII
1939	MCMXXXIX
1940	MCMXL
1941	MCMXLI
1942	MCMXLII
1943	MCMXLIII
1944	MCMXLIV
1945	MCMXLV
1946	MCMXLVI
1947	MCMXLVII
1948	MCMXLVIII
1949	MCMXLIX
1950	MCML
1951	MCMLI
1952	MCMLII
1953	MCMLIII
1954	MCMLIV
1955	MCMLV
1956	MCMLVI
1957	MCMLVII
1958	MCMLVIII
1959	MCMLIX
1960	MCMLX
1961	MCMLXI
1962	MCMLXII
1963	MCMLXIII
1964	MCMLXIV
1965	MCMLXV
1966	MCMLXVI
1967	MCMLXVII
1968	MCMLXVIII
1969	MCMLXIX
1970	MCMLXX
1971	MCMLXXI
1972	MCMLXXII
1973	MCMLXXIII
1974	MCMLXXIV
1975	MCMLXXV
1976	MCMLXXVI
1977	MCMLXXVII
1978	MCMLXXVIII
1979	MCMLXXIX
1980	MCMLXXX
1981	MCMLXXXI
1982	MCMLXXXII
1983	MCMLXXXIII
1984	MCMLXXXIV
1985	MCMLXXXV
1986	MCMLXXXVI
1987	MCMLXXXVII
1988	MCMLXXXVIII
1989	MCMLXXXIX
1990	MCMXC
1991	MCMXCI
1992	MCMXCII
1993	MCMXCIII
1994	MCMXIV
1995	MCMXV
1996	MCMXVI
1997	MCMXCVII
1998	MCMXCVIII
1999	MCMXXIX
2000	MM
2001	MMI
2002	MMII
2003	MMIII
2004	MMIV
2005	MMV
2006	MMVI
2007	MMVII
2008	MMVIII
2009	MMIX
2010	MMX
2011	MMXI
2012	MMXII
2013	MMXIII
2014	MMXIV
2015	MMXV
2016	MMXVI
2017	MMXVII
2018	MMXVIII
2019	MMXIX
2020	MMXX
2021	MMXXI
2022	MMXXII

Centuries in Roman Numerals

Century	Years
XI	1001 to 1100
XII	1101 to 1200
XII	1201 to 1300
XIV	1301 to 1400
XV	1401 to 1500
XVI	1501 to 1600
XVII	1601 to 1700
XVIII	1701 to 1800
XIX	1801 to 1900
XX	1901 to 2000
XXI	2001 to 2200

Fun Facts About Roman Numbers

In the Roman numerical system, does not exist representation of the number 0. As much as it was possible to represent quantities like 1000, they used only the letters to represent empty units, tens or hundreds. For example, the number 101 is represented by CI, even though it has zero tens, for the Romans it is not it used the decimal base as we do today, so the numbers were fine represented.

solved exercises

Question 1 - The correct representation of the number 758 in Roman numerals is:

A) VIIIVIII

B) DCCLIIIV

C) DCCLVIII

D) CCDLIVI

E) CCCMLVIII

Resolution

Alternative C

To represent the number 758, we use the symbols:

DCCLVIII → 500 + 100 + 100 + 50 + 8 = 758

Question 2 - The decimal base representation of the sum MDCXII with MDIX is equal to:

A) 3612

B) 3021

C) 3191

D) 3021

E) 3121

Resolution

Alternative E

MDCXII → 1000 + 500 + 100 + 12 = 1612

MDIX → 1000 + 500 + 9 = 1509

1612 + 1509 = 3121

By Raul Rodrigues de Oliveira
Maths teacher