THE cientific notation is a widely used tool not only in Mathematics, but also in Physics and Chemistry. It allows us to write and operate numbers that, when written in their original form, require great patience and effort, as they are either very large numbers or very small numbers. Imagine, for example, you writing the distance between the planet Earth it's the Sun in kilometers or writing the charge of a proton in coulomb.
In this text, we will explain how represent these numbers in a simpler way and some of its features.
Read too:Astronomical units: what are they?
How to turn a number into scientific notation

To transform a number into scientific notation, it is necessary to understand what they are. base 10 powers. From the definition of power, we have to:
100 = 1
101 = 10
102 = 10 · 10 = 100
103 = 10 · 10 · 10 = 1.000
104 = 10 · 10· 10· 10 = 10.000
105 = 10· 10· 10· 10· 10 = 100.000
Note that insofar as the exponent increases
, also increase the amount of zeros of the answer. Also see that the number in the exponent is the amount of zeros we have to the right. This is equivalent to saying that the number of decimal places moved to the right is equal to the power exponent. For example, 1010 is equal to 10,000,000,000Another case that we must analyze is when the exponent is a negative number.
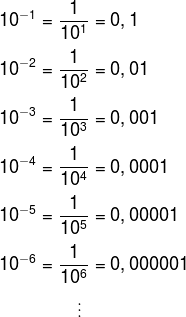
Note that when the exponent is negative, the decimal places appear to the left of the number, that is, we “walk” decimal places to the left. Also see that the number of decimal places moved to the left coincides with the power exponent. THE number of zeros to the left of the number 1 therefore coincides with the number of the exponent.The power 10 –10, for example, is equal to 0.0000000001.
Do not stop now... There's more after the advertising ;)
Revised the idea of power of base 10, let's now understand how to transform a number into scientific notation. It is important to emphasize that, regardless of the number, to write it in the form of scientific notation, we must always leave it with a significant figure.
So, to write a number in scientific notation form, the first step is to write it in product form, so that a power of base 10 (decimal form) appears. See the examples:
a) 0.0000034 = 3,4 · 0,000001 = 3,4 ·10 – 6
b) 134,000,000,000 = 134 · 1.000.000.000 = 134 · 109
Let's agree that this process is not practical at all, so in order to make it easier, please note that, when we "walk" with the comma to the right, the exponent of base 10 decreases the number of decimal places walked. Now, when we "walk" decimal places to the left, the exponent of base 10 increases the amount of houses walked.
In summary, if zeros are to the left of the number, the exponent is negative and coincides with the number of zeros; if zeros appear to the right of the number, the exponent is positive and also matches the number of zeros.
Examples
a) The distance between planet Earth and the Sun is 149,600,000 km.
Note the number and see that, to write it in scientific notation, it is necessary to "walk" with the decimal point eight decimal places to the left, so the base 10 exponent will be positive:
149.600.000 = 1,496 · 108
b) The approximate age of planet Earth is 4,543,000,000 years.
Similarly, note that to write the number in scientific notation, it is necessary to move 9 decimal places to the left, therefore:
4.543.000.000 = 4,543· 109
c) The diameter of an atom is of the order of 1 nanometer, that is, 0.0000000001.
To write this number using scientific notation, we must go 10 decimal places to the right, therefore:
0,0000000001 = 1 · 10-10
Read too: International System of Units: the standardization of measurement units
Operations with scientific notation
To operate on two numbers written in scientific notation, we first have to operate on the numbers that follow the powers of 10 and then operate on the powers of 10. For this, it is necessary to keep in mind the properties of potencies. The most used are:
Product of powers of the same base:
Them ·Theno = them + n
Powers quotient of the same base:

Power of a power:
(Them)no = them ·n
Examples
a) 0.00003 · 0.0027
We know that 0.00003 = 3 · 10 – 5 and that 0.0027 = 27 · 10 – 4 , so we have to:
0,00003 · 0,0027
3 · 10 – 5 · 27 · 10 – 4
(3 · 27) · 10 – 5 + (– 4)
81· 10 – 9
0,000000081
b) 0.0000055: 11,000,000,000
Let's write the numbers using scientific notation, so 0.0000055 = 55 · 10 – 7 and 11,000,000,000 = 11 · 109.
0,0000055: 11.000.000.000
55 · 10 – 7 : 11 · 109
(55: 11) · 10 (– 7 – 9)
5 · 10 – 16
0,0000000000000005
solved exercises
question 1 – (UFRGS) Considering a proton as an edge cube 10 – 11 m and mass 10 – 21 kg, what is its density?
Solution
We know that the density is the ratio between mass and volume, so it is necessary to calculate the volume of this proton. As the shape of the proton according to the statement is a cube, the volume is determined by: V = a3, on what The is the measure of the edge.
V = (10 – 11)3
V = 10 – 33 m3
Density is therefore:
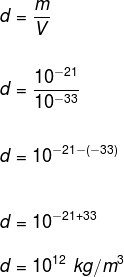
question 2 – The speed of light is 3.0 · 108 m/s. The distance between the Earth and the Sun is 149,600,000 km. How long does sunlight take to reach Earth?
Solution
We know that the relationship between distance, speed and time is determined by:
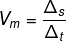
Before substituting the values in the formula, note that the speed of light is in meters per second, and the distance between the Earth and the Sun, in kilometers, that is, it is need to write this distance in meters. For that, let's multiply the distance by 1000.
149.600.000 · 1000
1,496 · 108· 103
1,496 · 108+3
1,496 · 1011 m
Now, replacing the values in the formula, we have:
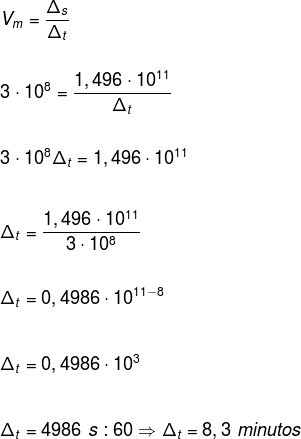
by Robson Luiz
Maths teacher



