Circle and circumference: concepts and elements

THE circumference and the circle are pictures flat geometrics that appear frequently in nature. just like the others geometric shapes have their elements, the circumference and the circle too have some special features.

See too: Point, Line, Plane and Space: Basic Concepts of Geometry

What is circumference?

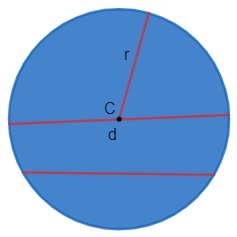
One circumference is a region of the plane formed by points that are equidistant from a fixed point called the center of the circle, that is, it is formed by points that are the same distance from the center.

The point in the middle of the circle is the center. Note that the distance between all blue dots to the center is the same.

elements of the circle

In every circumference, we have lightning, diameter and rope. Now let's look at each of these elements:

O lightning (r) of the circumference is the straight segment which joins the center (C) of the circle to its end (in blue). The line segment that joins the two ends of the circle and passes through the center Ç it's called diameter of the circumference and is denoted by the letter

d. Note that the diameter is the sum of the radius of the circle, so:

d = r + r

d = 2·r

As can be seen, the diameter is twice the radius. Any other line segment that joins two ends of the circle and that does not pass through the center is called a rope.

Do not stop now... There's more after the advertising ;)

• Example

Determine the radius of a circle that has a diameter equal to 20 cm.

As the diameter is twice the radius, we have:

In other words, the radius is half the diameter.

The circle and circle have a strict relationship.

Circumference perimeter

The perimeter of the circumference, also called the circumference length, will be represented by C. Imagine making a cut at any point on the circumference and “stretching” it until a straight line segment is found. What we're going to do now is determine the size of this line segment.

The Greek mathematician and philosopher Archimedes, in one of his studies, realized that reason between circumference length ( C ) and diameter (d) always resulted in the same number. This constant was called pi, which is denoted by the symbol π.

From this ratio between the length of the circumference and the diameter, we can find an expression that makes it possible to determine the length of the circumference or perimeter as a function of the radius. Look:

We know that the diameter of the circle is twice the radius, that is, d = 2r. Substituting this value in the expression above, we will have that the length of the circle as a function of the radius measure is:

C = π · 2r

C = 2πr

We usually use the value of pi to be 3.14.

• Example

Determine the length of a circumference of radius 25 cm.

Substituting the radius value in the formula, we have:

C = 2πr

C = 2(3.14)(25)

C = 157 cm

What is the circle?

The definition of a circle derives from the definition of a circle, as a circle is the inner region of the circle. Making a comparison, we have that the circumference is the extremity, and the circle is the entire region delimited by this extremity. See the picture:

The entire region painted in blue is called a circle.

Read too: Angles in the circle: how to find them?

circle elements

• As the circle is a region of the plane determined by a circle, the elements of the circle coincide with the elements of the circle, that is, it also has lightning, diameter and rope. Look:

circle area

THE circle area it is the measure of the entire region delimited by the circumference. Consider a circle of radius a:

The area of ​​the circle is given by:

• Example

A circle has a radius equal to 5 cm. Determine your area.

Resolution:

Substituting the radius value in the formula, we have:

A = πr²

A = (3.14) 5²

A = 3.14 · 25

H = 78.5 cm²

See too: circumference length and circle area

solved exercises

question 1 – A circumference has a perimeter equal to 628 cm. Determine the diameter of this circle and adopt π = 3.14.

Solution

Since the perimeter is equal to 628 cm, we can substitute this value in the circumference length expression.

question 2 – Two circles are concentric if they have the same center. Knowing this, determine the area of ​​the blank figure.

Solution:

To determine the area in white, we must calculate the area of ​​the larger circle and subtract the area of ​​the blue circle.

THE_BIGGER = r²

THE_BIGGER = (3,14) · (9)²

THE_BIGGER = (3,14) · 81

THE_BIGGER = 254.34 cm²

Let's now calculate the area of ​​the blue circle:

THE_BLUE = r²

THE_BLUE = (3,14) · (5)²

THE_BLUE = (3,14) · 25

THE_BLUE = 78.5 cm²

So the white area is the difference between the larger area and the blue area.

THE_WHITE = 254,34 – 78,5

THE_WHITE = 175.84 cm²

by Robson Luiz
Maths teacher

Would you like to reference this text in a school or academic work? Look:

LUIZ, Robson. "Circle and circumference"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/circulo-ou-circunferencia.htm. Accessed on June 27, 2021.