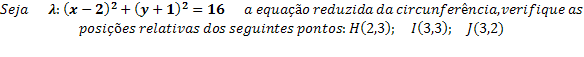THE circumference is a flat geometric figure formed by union of equidistant points, that is, they have the same distance from a fixed point called the center. The study of the circumference is also present in the analytic geometry, in which it is possible to deduce an equation that represents it.
although the circle and circumference are flat geometric figures with some elements in common, which usually leads to doubts, these figures present important differences, especially with regard to dimensionality.
Read too: Distance between two points - an important concept of analytic geometry
elements of the circle
Note the circumference:

The point Ç it's called center of the circle, and note that points A and B belong to it. The segment that joins the ends of the circle passing through the center is called the diameter. On the previous circumference, then we have to the diameter is the AB segment.
To the divide the diameter in half, let's get the radius of the circumference, that is, the radius (r) of a circle
it is the segment that joins the center and the end. In this case, the radius is the CB segment. We can establish a mathematical relationship between these two elements, since the diameter is twice the radius.d = 2 · r
Do not stop now... There's more after the advertising ;)
Example
Determine the radius of a circle that has a diameter measuring 40 cm.
We know that the diameter is twice the radius, like this:
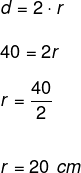
circumference length
Consider a circle that has a radius measuring r. O length or perimeter of the circumference is given by the product of the çconstant pi (π) by twice the radius.
When we calculate the length or perimeter of a circle, we are determining the size of the line green in the previous drawing, and to do this, just replace the radius value in the formula that proceeds to figure.
Example
Determine the length of the circumference of radius 5 cm.
The radius of the circle equals 5 cm, so to determine the length of the circle, we must substitute this value in the formula.
C = 2πr
C = 2(3.14)(5)
C = 6.24 · 5
C = 31.2 cm
See too: Construction of inscribed polygons
circumference area
Consider a circle of radius r. To calculate your area, we must multiply the square of the radius value by π.

When we calculate the area of the circle, we are determining the surface measure, that is, the entire region inside the circle.
- Example
Determine the area of a circle that has a radius equal to 4 cm.
We have that the radius of the circumference is equal to 4 cm, so we can substitute this measure in the formula for the area. Look:
A = π · r2
A = 3.14 · (4)2
A = 3.14 · 16
H = 50.24 cm2
Circumference reduced equation
We know that a circle can be built by collection of points that have the same distance from a fixed point called the origin or center. So, consider a fixed point in the Cartesian plane O(a, b). The set of points — represented by P(x, y) — that are the same distance r from this fixed point will form a circle of radius r.
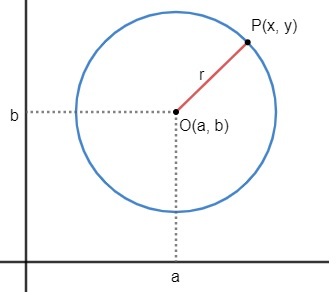
Note that the points of the form P(x, y) are all the same distance from point O(a, b), ie, the distance between the points O and P is equal to the radius of the circle, thus:

At reduced equation, note that the numbers The and B are the coordinates of the center of the circle and that r is the measure of the radius.
- Example
Determine the coordinates of the center and the measure of the radius of the circle that has an equation:
a) (x – 2)2 + (y – 6)2 = 36
Comparing this equation with the reduced equation, we have:
(x – The)2 + (y – B)2 = r2
(x – 2)2 + (y –6)2 = 36
See that a = 2, b = 6 and r2 = 36. The only equation to solve is:
r2 = 36
r = 6
Therefore, the coordinate of the center is: O(2, 6) and the radius length is 6.
b) (x – 5)2 + (y + 3)2 = 121
Similarly, we have:
(x – The)2 + (y – B)2 = r2
(x – 5)2 + (y + 3)2 = 121
a = 5
– b = 3
b = –3
While the radius value is given by:
r2 = 121
r = 11
c) x2 + y2 = 1
(x – The)2 + (y – B)2 = r2
x2 + y2 = 1
Note that x2 = (x + 0)2 and y2 = (y + 0)2 . So we have to:
(x – The)2 + (y – B)2 = r2
(x + 0)2 + (y + 0)2 = 1
Therefore, the coordinate of the center is O(0, 0) and the radius is equal to 1.
Also access: How to find the center of a circle?
general equation of the circle
To determine the general equation of the circle, we must develop the reduced equation her. Thus, consider a circle that has a center at the coordinates O(a, b) and radius r.
Initially, we will develop the terms squared using the notable products; then we'll pass all numbers to the first member; and, finally, we will join the terms with the same literal coefficient, that is, those with the same letters. Look:
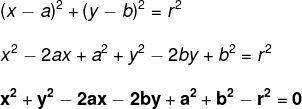
Example
Determine the coordinates of the center and the mean radius of the circle that has an equation:
a) x2 + y2 – 4x – 6y + 4 + 9 – 49 = 0
To determine the radius and coordinates of the circle that has this equation, we must compare it with the general equation. Look:
x2 + y2 – 2ndx - 2by + The2 + B2 –r2 = 0
x2 + y2 – 4x - 6y + 4 + 9 – 49 = 0
From the comparisons in green, we have to:
2nd = 4
a = 2
or
The2 = 4
a = 2
From the comparisons in red, we have that:
2b = 6
b = 3
or
B2 = 9
b =3
Thus, we can say that the center has coordinate O(2, 3). Now, comparing the value of r, we have:
r2 = 49
r = 7
Therefore, the radius of the circle has a length equal to 7.
b) x2 + y2 – 10x + 14y + 10 = 0
In a similar way, let's compare the equations:
x2 + y2 – 2ndx - 2by + The2 + b2 – r2 = 0
x2 + y2 –10x + 14y + 10 = 0
2nd = 10
a = 5
Determining the value of b:
–2b = 14
b = – 7
Note now that:
The2 + b2 – r2 = 10
Since we know the values of a and b, we can substitute them in the formula. Look:
The2 + b2 – r2 = 10
52 + (–7)2 – r2 = 10
25 + 49 - r2 = 10
74 – r2 = 10
– r2 = 10 – 74
(–1) – r2 = –64 (–1)
r2 = 64
r = 8
Therefore, the coordinates of the center are O (5, –7) and the radius has a length equal to 8.

Differences between circumference and circle
The difference between a circle and a circle concerns the number of dimensions of each element. While the circle has one dimension, the circle has two.
A circle is a region in the plane formed by points all equidistant from a fixed point called the origin. The circle is made up of every region within the circle. See the difference in images:

See too:circumference length and circle area
solved exercises
question 1 – A circumference has a perimeter equal to 628 cm. Determine the diameter of this circle (adopt π = 3.14).
Resolution
Since the perimeter is equal to 628 cm, we can substitute this value in the circumference length expression.

question 2 – Two circles are concentric if they have the same center. Knowing this, determine the area of the blank figure.
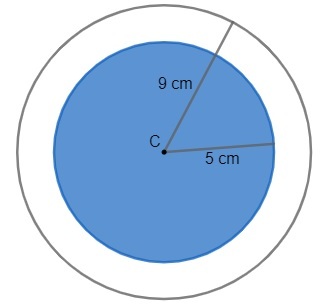
Resolution
Note that to determine the area of the region in white, we must determine the area of the larger circle and then that of the smaller circle in blue. Also note that if we remove the blue circle, only the region we want is left, so we must subtract those areas. Look:
THEBIGGER = r2
THEBIGGER = (3,14) · (9)2
THEBIGGER = (3,14) · 81
THEBIGGER = 254.34 cm2
Let's now calculate the area of the blue circle:
THESMALLER = r2
THESMALLER = (3,14) · (5)2
THESMALLER = (3,14) · 25
THESMALLER = 78.5 cm2
Thus, the blank area is given by the difference between the larger area and the smaller area.
THEWHITE = 254,34 – 78,5
THEWHITE = 175,84 cm2
by Robson Luiz
Maths teacher
Regarding the basic definition of circles and their properties, tick the correct alternative.
a) A circle is a flat region bounded by a circle.
b) A circle is a set of points whose distance to the center is always smaller than the constant r.
c) A circle has only two radii and the sum of these two elements is equal to the diameter.
d) A circle with center O and radius r is a set of all points whose distance to O is equal to r.
e) Circle is the region of the plane limited by a diameter.
a) Given a point A, outside the circumference, the segment OA is less than or equal to r.
b) Knowing that the segment OA has a length shorter than r, it can be said that A belongs to the circle limited by this circumference.
c) Knowing that the segment OA has a length greater than r, it can be stated that A belongs to the circle.
d) The diameter of the circle bounded by this circumference is equal to 3r.
e) For point A to belong to the circle, it is enough that the distance from A to O be smaller than r.